A wire loop enclosing a semicircle of radius R islocated on the boundary of a uniform magnetic field B. At the moment t=0, the loop is set into rotation with constant angular acceleration α about an axis O. The clockwise emf direction is taken to be positive.
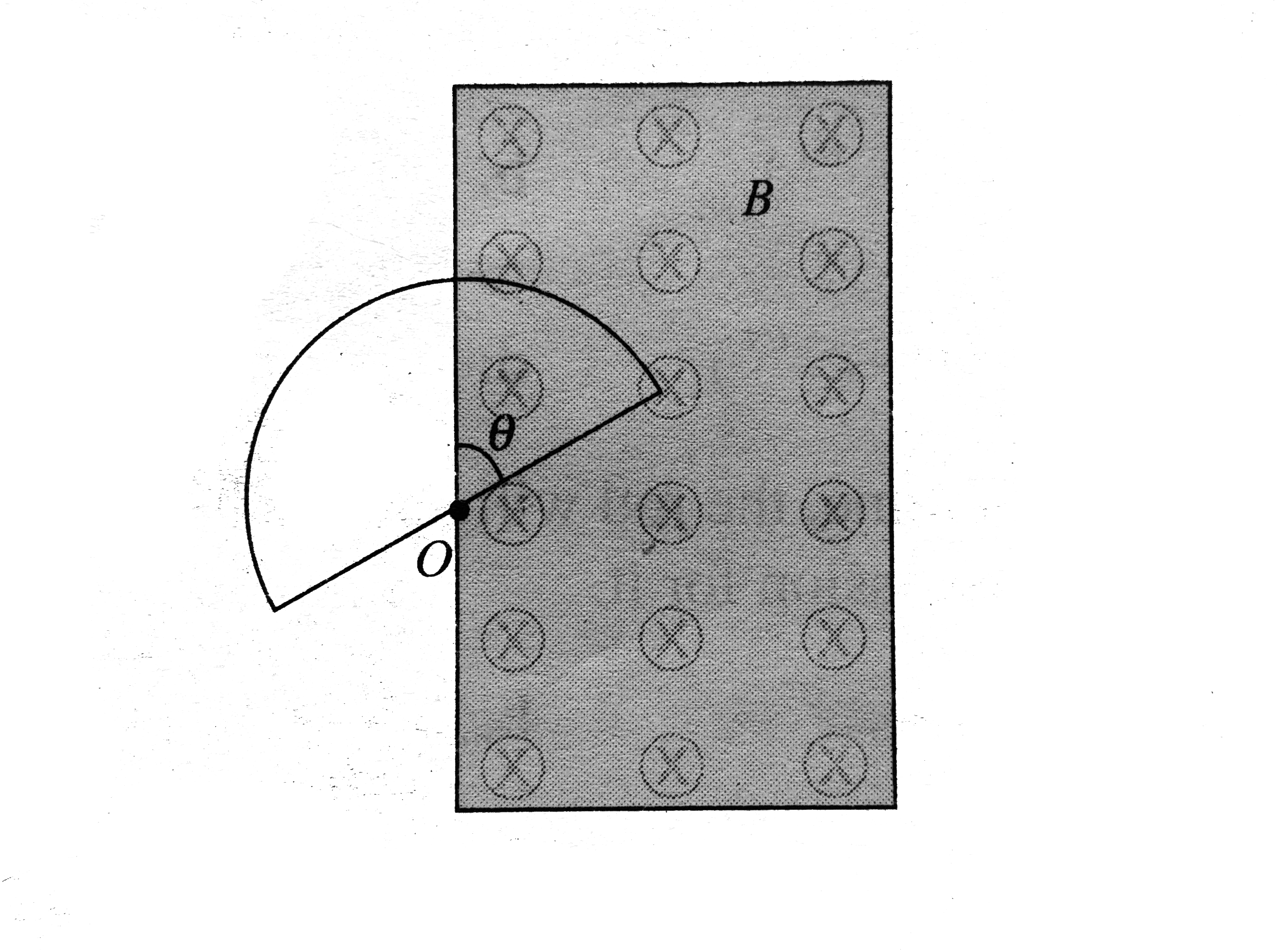
The variation of emf as function of time is
(a) 12BR2αt
(b) 32BR2αtA
( c) √3BR2αt
(d) BR2αt√2
The correct Answer is:A
(a)emf is induced in the loop because area inside the magnetic field is continually changing.
From θ=0→π, 2π→3π, 4π→5π, the loop beings to enter the magnetic field. Thus the magnetic field passing through the loop is increasing.Hence, current in the loop is anticlockwise, and for θ=π to2π, 3π to 4π, 5π to 6π, etc. magnetic field passing through the loop is decreasing. Hence current in the loop is clockwise. Let at any time, angle rotated is θ, then θ=12αt2
Area inside magnetic field. A=12R2θ=12R2(12αt2)=14R2αt2
Flux in the loop: ϕ=BA=B4R2αt2
emf: e=−dϕdt=−B2R2αt → e∝t
Time taken to complete first half circle: t1=√2πα
When within magnetic field:
A=12R2(2π−θ)=πR2−R2θ2
emf e=−dϕdt=B2R2αt
e=−BR22=αt → e ∝t
Time taken to complete second half revolution
t2=√4πα=√2πα
We see that t2<t1
We can write induced emf as e=(−1)n[12BR2αt]
Where n=1,2,3,...... is the number of half revolution completed by loop Smaller time will be taken to complete the second half revolution as compared to the previous half revolution.


Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Integer
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Archives Fill In The Blanks
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:CENGAGE PHYSICS ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercises Asserton - Reasoning
Explore 8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
Similar Questions
A wire loop enclosing a semicircle of radius R islocated on the boundary of a uniform magnetic field B. At the moment t=0, the loop is set into rotation with constant angular acceleration α about an axis O. The clockwise emf direction is taken to be positive.
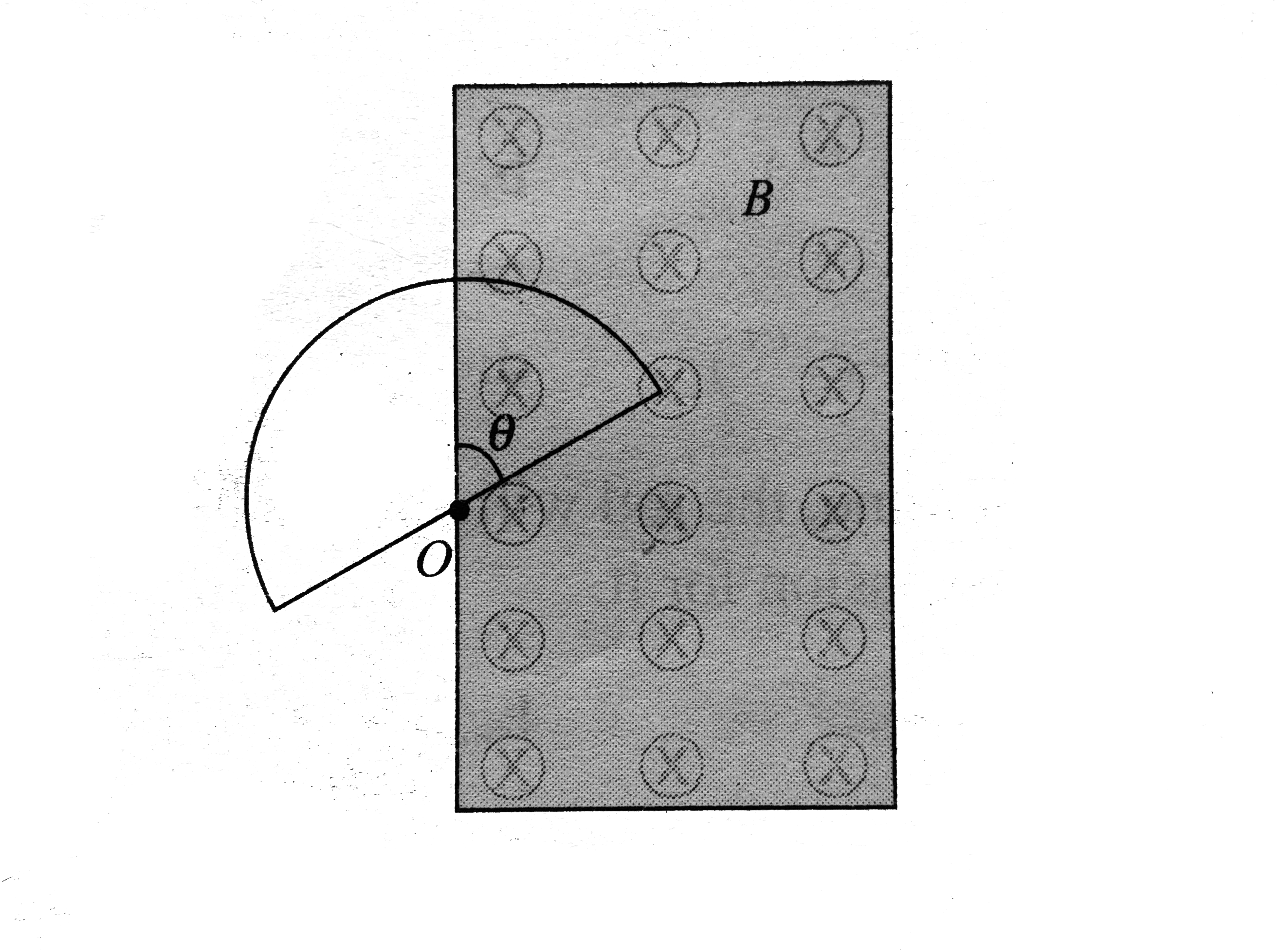

The variation of emf as a function of time is
View SolutionA wire loop enclosing as semicircle of radius R is located on the boudary of uniform magnetic field B. At the moment t=0, the loop is set into rotation with a costant angular acceleration α about an axis O coinciding with a line of vector B on the boundary. Find the emf induced in the loop as a function of time. Draw the approximate plot of this function.The arrow in the figure shows the emf direction taken to be positive.
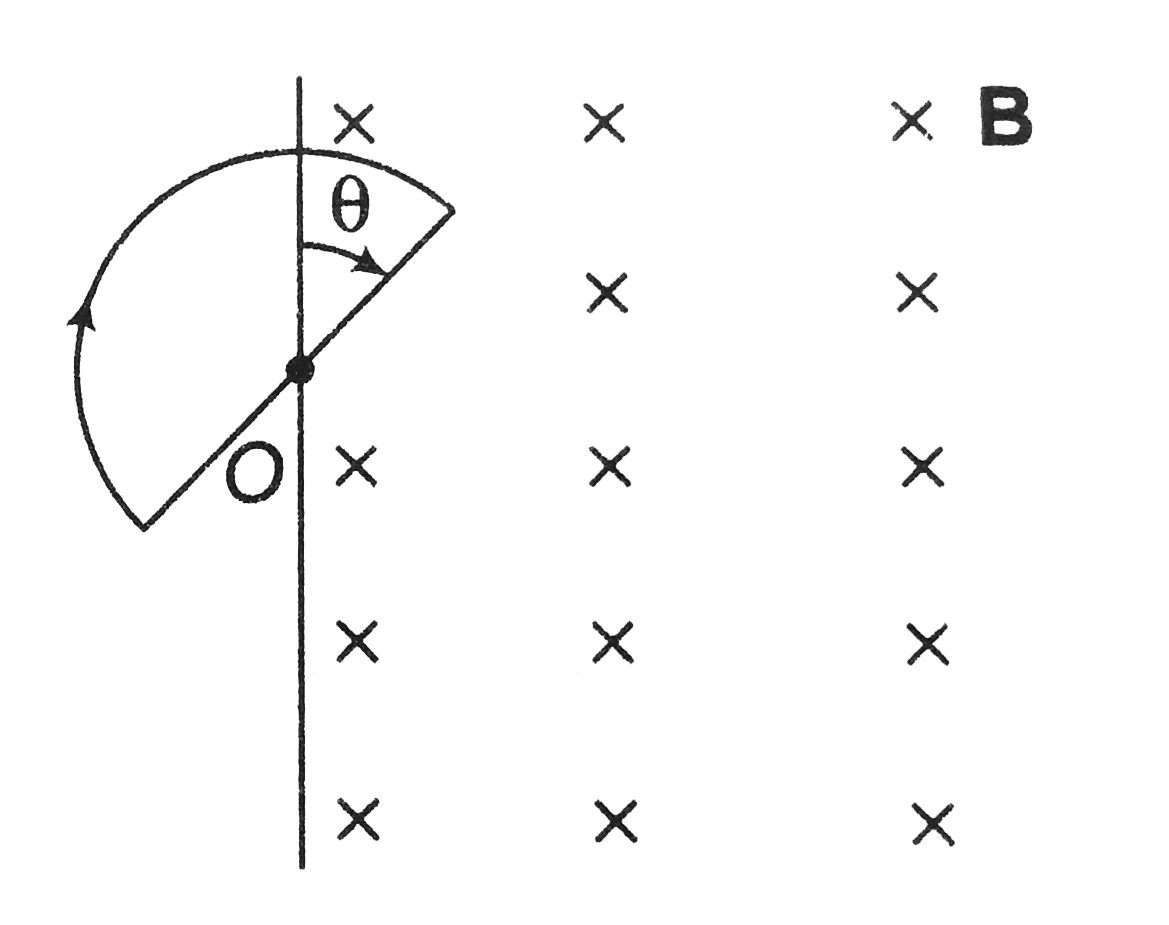
View SolutionA wire loop enclosing a semi-circle of radius a=2cm is located on the boundary of a uniform magnetic field of induction B=1T (figure).At the moment t=0 the loop is set into rotation with a constant angular acceleration β=2rad/sec2 about an axis O coinciding with a line of vector B on the boundary.The emf induced in the loop as a function of time t is [x×10−4(−1)n×t]V, where n=1,2,... is the number of the half-revolution taht the loop performs at the given moment t.Find the value of x.(The arrow in the figure shows the emf direction taken to be positive, at t=0 loop was completely outside)

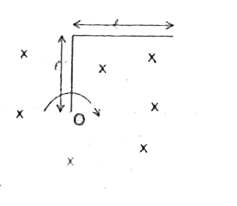
View SolutionFor the L shaped conductor in a uniform magnetic field B shown in figure the emf across its ends when it rotates with angular velocity ω about an axis through one its ends O and normal to its plane will be
View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionA circular wire loop of radius r is placed in a region of uniform magnetic field B such that the plane of the loop makes an angle θ with the direction of B. In which of the following conditions, will no emf be induced in the loop?
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View Solution
