A wire of uniform cross - section is suspended vertically from a fixed point , with a load attached at the lower end . Calculate the fractional change in frequency of the wire due to rise in temperature by t∘C. The coefficient of expansion of the wire is α.
With a temperature change , the tension and mass of the wire will not change but length (I) and linear density (m) will change.
n=12√TMandm=MI
Where M = mass of the wire
∴N=12√TMI=k√I
where k=12√T/M=a(constant)
Differentiating both sides
Δn=k(−12)I−3/2ΔI
∴Δnn(tionalchan≥)=12KI−3/2ΔIKI−1/2
or Δnn=12ΔII=12αt(ΔI=I∝t)
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Subjective
Explore 24 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Single Correct
Explore 144 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Comprehension Type
Explore 5 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
Two wires of different linear mass densities are soldered together end to end and then stretched under a tension F. The wave speed in the first wire is thrice that in the second. If a harmonic wave travelling in the first wire is incident on the junction of the wires and if the amplitude of the incident wave is A=√13cm, find the amplitude of reflected wave.
View SolutionThe displacement of a particle is given by x=3sin(5πt)+4cos(5πt). The amplitude of particle is
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionDuring the adiabatic expansion of 2 moles of a gas, the internal energy of the gas is found to decrease by 2 joules , the work done during the process on the gas will be equal to
View SolutionOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View SolutionA wire of uniform cross - section is suspended vertically from a fixed point , with a load attached at the lower end . Calculate the fractional change in frequency of the wire due to rise in temperature by t^(@) C . The coefficient of expansion of the wire is alpha .
View SolutionOne end of a uniform wire of length 'L' and mass 'M' is attached rigidly to a point in the roof and a load of a mass 'm' is suspended from its lower end. If A is the area of cross-section of the wire then the stress in the wire at height 'x' from its lower end (x lt L) is
View SolutionOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight N is suspended from its lower end if s is the area of cross-section of the wire the stress in the wire at a height (L)/(4) from its lower end is
View SolutionOne end of a uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross-section of the wire, the stress in the wire at a height 3 L/4 from its lower end is
View SolutionOne end of uniform wire of length Land of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area if cross-section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and a weight W/2 is suspended from the lower end. If A is the area fo cross-section of the wire, then stress of the wire at its midpoint will be
View SolutionA wire ofuniform cross-section is suspended vertically from a fixed point , with a load attached at the lower end. Show that the change in frequency related to the altered frequency of the wire due to rise in temperature is approx (1)/(2) alpha t, Where alpha is the linear coefficient of expansion of the wire and t^(@)C is small rise in temperature.
View SolutionOne end of a uniform wire of length L and weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
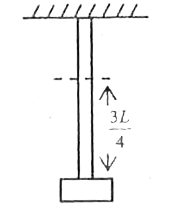
View SolutionOne end of a uniform wire of length .L. and mass .M. is attached rigidly to a point in the roof and a load of mass .m. is suspended from its lower end. If A is the area of corss - section of the wire then find the stress in the wire at height .x. from its lower end (x<L)
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and weight W /2 is suspended from the lower end. If A is the area of cross section of the wire then stress in the wire at its mid point is
View Solution
