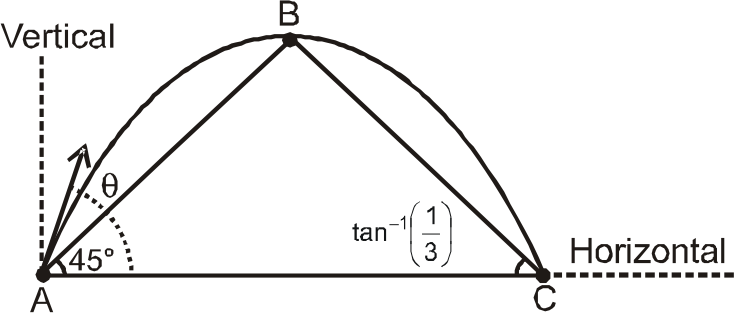
ABC is a triangle in vertical plane. Its two base angles ∠BAC and ∠BCA are 45∘ and tan−113 respectively. A particle is projected from point A such that is passes through vertices B and C. Angle of projectio is θ. Find the value of 3tanθ.

The correct Answer is:4
Step by step video solution for ABC is a triangle in vertical plane. Its two base angles /_BAC and /_BCA are 45^(@) and "tan"^(-1)1/3 respectively. A particle is projected from point A such that is passes through vertices B and C. Angle of projectio is theta. Find the value of 3 tan theta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If two angles of a triangle are tan−112andtan−113 . Then the third angle is
Aπ4B5π4Cπ2D3π4
If θ is an acute angle and sinθ=cosθ , find the value of 2tan2θ+sin2θ−1
View SolutionThe points A(3,0) , B (a, -2) and C(4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
View SolutionThe points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B, Find the values of P.
View SolutionIf tan2θ= 1−e2 then the value of secθ+tan3θcosecθ
View SolutionProve that the points A (1,-3) B (-3,0) and C(4,1) are the vertices of an isosceles right angle triangle. Find the area of the triangle.
View SolutionA triangle ABC is right angled at B. Find the value of secA.sinC−tanA.tanCsinB
View SolutionIf θ is an acute angle and tanθ+secθ=1.5, find sinθ,tanθ and secθ.
View Solution