An ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
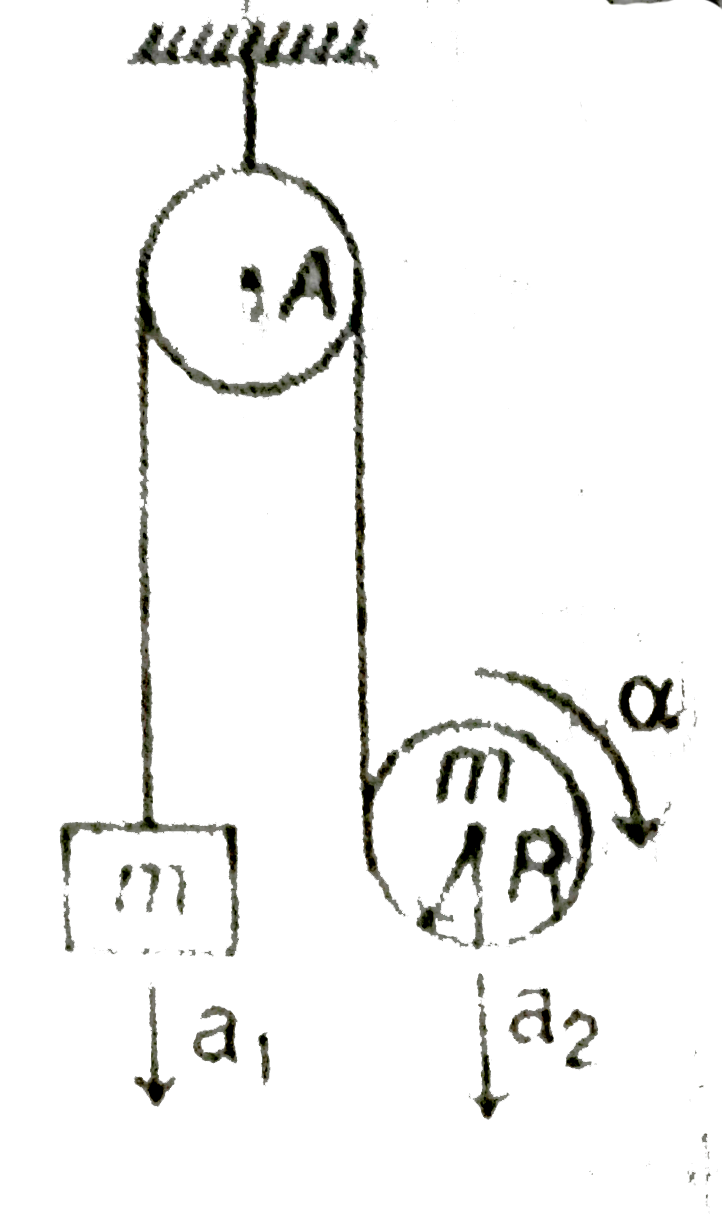
a1=a2
αR>a1
αR=a1
αR<a2
The correct Answer is:D
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:More than one option is correct
Explore 36 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Comprehension Type Questions
Explore 41 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
Similar Questions
Which of the following statement (s) is / are correct for a spherical body rolling without slipping on a rough horizontal ground at rest?
View SolutionA rod of length 2 m is kept vertical inside a smooth spherical shell of radius 2m. The rod starts slipping inside the shell . Mass of the rod is 4 kg.
Angular speed of the rod(in rad/s) in the position when it becomes horizontal is

View SolutionA ring and a disc having the same mass, roll without slipping with the same linear velocity. If the kinetic energy of the ring is 8 j , Find the kinetic energy of disc (in J)
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionWhen an electric field is applied across a semiconductor,
View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
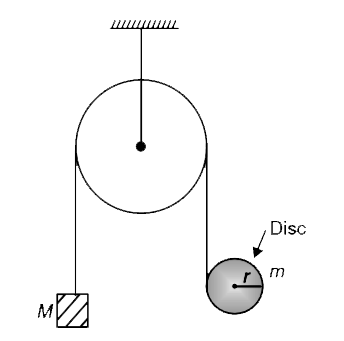
View SolutionA mass less string is wrapped around a uniform disc of mass m and radius r. The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc.
(a) Find the acceleration of the block for the case M=m
(b) Find Mm for which the block can accelerate upwards.
View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
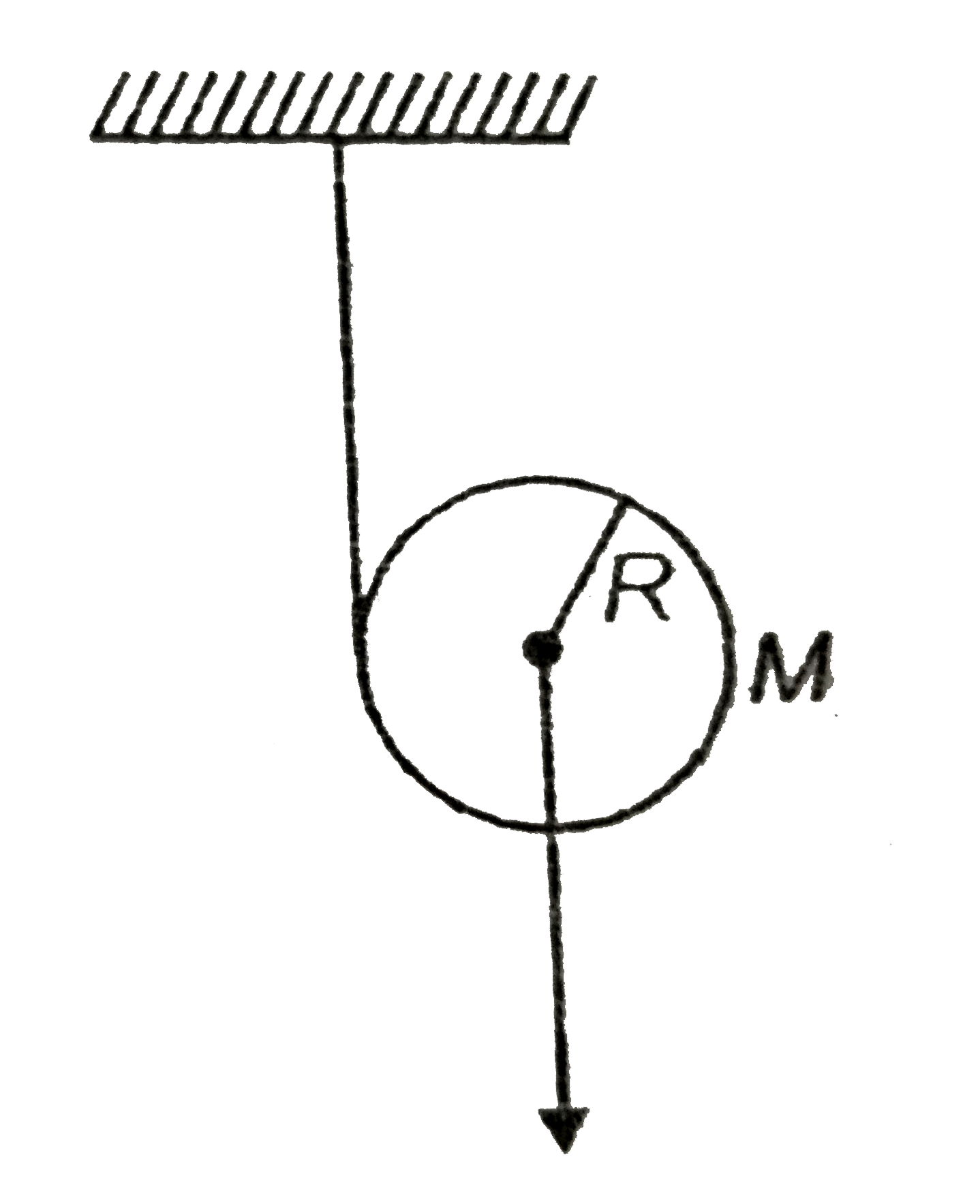
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
View SolutionThe masses M and m connected to the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given, M gt m .
View SolutionA mass m hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m if the string does not slip on the pulley, is
View Solutionएक घर्षणहीन बेयरिंग पर एक घिरनी के चारों ओर एक डोरी को लपेट कर द्रव्यमान m लटकाया गया है। घिरनी का द्रव्यमान m और त्रिज्या R है। यह मान लें कि घिरनी एक पूर्ण एकसमान वृतीय चकती है। यदि डोरी घिरनी पर फिसलती नहीं है, तब द्रव्यमान m का त्वरण है
View SolutionThe mass m is hung by wrapping a string around a pulley on a frictionless bearing. The mass of the pulley is m and radius R. Assume that the pulley is a perfectly uniform circular disc. If the string does not slide on the pulley, then the mass m is acceleration.
View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View Solution

