An organ pipe of length L open at both ends is found to vibrate in its harmonic when sounded with a tuning fork of 480Hz. What should be the length of a pipe closed at one end, so that it also vibrates in its first harmonic with the same tuning fork?
Consider the situation shown in the diagram
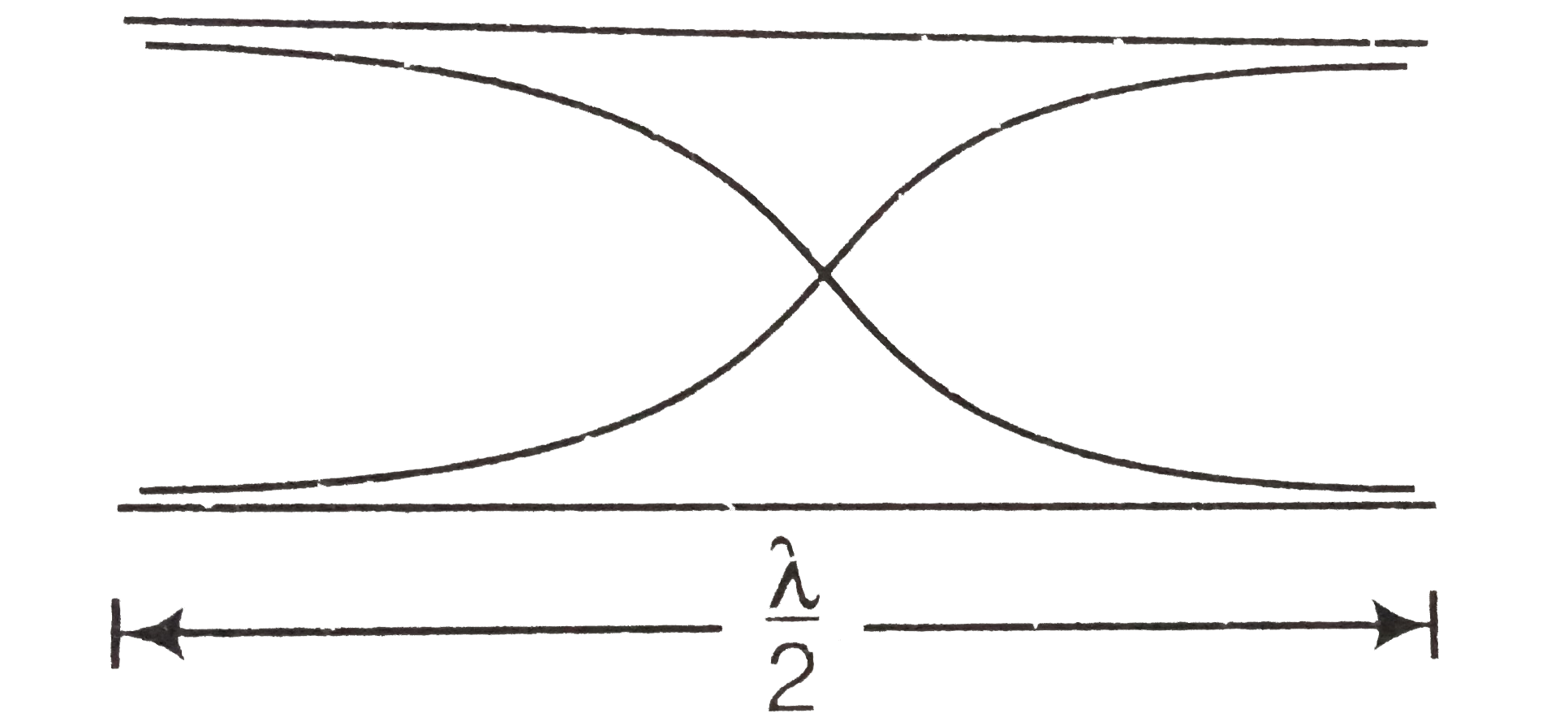
As the organ pipe is open at both ends, hence for first harmonic
l=λ2
⇒ λ=2l⇒cv=2l⇒v=c2l
wherer c is speed of the sound wave in air .
For pipe closed at one end
v'=c4L'
c for harmonic
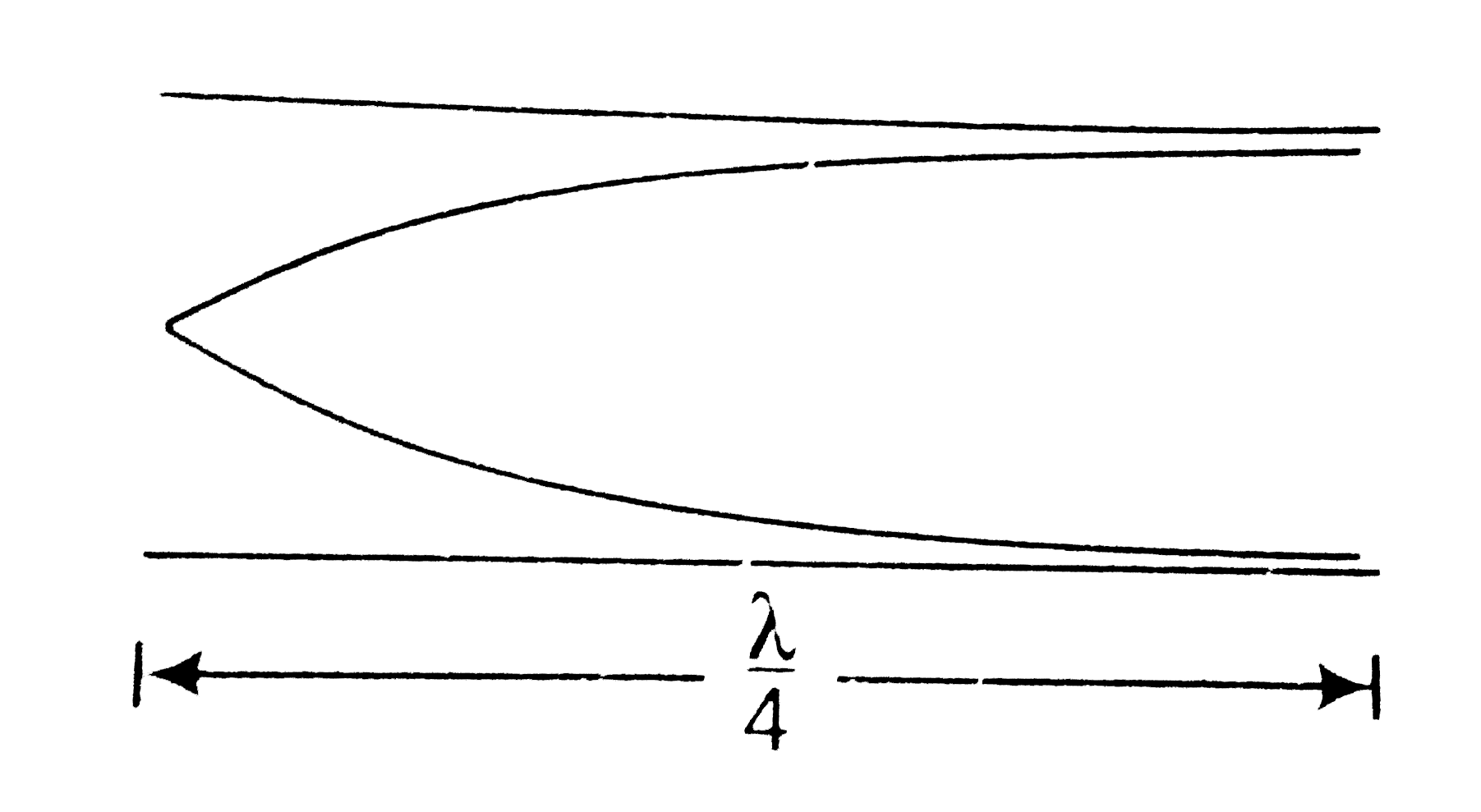
Hence v=v' [ for resonance wit same tuning fork]
⇒r c2L=c4L' [∴ speed remains constant ]
⇒ L'L=24=12⇒L'=L2
Topper's Solved these Questions
- WAVESBook:NCERT EXEMPLARChapter:WAVESExercise:SHORT ANSWER TYPE QUESTIONS
Explore 7 Videos
- WAVESBook:NCERT EXEMPLARChapter:WAVESExercise:LONG ANSWER TYPE QUESTIONS
Explore 5 Videos
- WAVESBook:NCERT EXEMPLARChapter:WAVESExercise:MULTIPLE CHOICE QUESTIONS (MORE THAN ONE OPTIONS )
Explore 7 Videos
- UNITS AND MEASUREMENTS Book:NCERT EXEMPLARChapter:UNITS AND MEASUREMENTS Exercise:Long Answer Type Questions
Explore 9 Videos
- WORK, ENERGY AND POWERBook:NCERT EXEMPLARChapter:WORK, ENERGY AND POWERExercise:Long answer
Explore 1 Video
Similar Questions
A steel wire has a length of 12 m and mass of 23.10 kg . What will be the speed of a transverse wave on this when a tension of 2.06×104N is applied?
View SolutionThe earth has a radius of 6400km. The inner core of 1000 km radius is solid. Outside it, there is a region from 1000 km to a radius of 3500km which is in molten state. Then again from 3500km to 6400 km, the earth is solid. Only longitudinal (P) waves can travel inside a liquid. Assume that the P wave has a speed of 8kms−1 in solid parts and of 5kms−1 in liquid parts of the earth. Calculate the time after which it will be recorded in a seismometer at a diametrically opposite point on earth if wave travels along diameter.
View SolutionA transverse harmonic wave on a string is described by y(x,t)=3.0sin(36t+0.018x+π/4) where x, y are in cm, t in second. The positive direction of x is from left to right . (i) Is this a travelling or stationary wave ? If travellying, what are the speed and direction of its propagation ? (ii) what are its amplitude and frequency ? (iii) what is the inital phase at the origing ? (iv) What is the least distance between two successive creests in the wave?
View SolutionA new system of units is proposed in which unit of mass is αkg, unit of length β m and unit of time λs. How much will 5 J measure in this new system ?
View SolutionA block of mass 1kg is pushed up a surface inclined to horizontal at an angle of 30∘ by a force of 10N parallel to the inclined surface [figure]. The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate
(a) work done against gravity
(b) work done against force of friction
(c) increase in potential energy
(d) increase in kinetic energy
(e) work done by applied force.

View SolutionAn organ pipe A closed at one end vibrating in its fundamental frequency and another pipe B open at both ends is vibrating in its second overtone are in resonance with a given tuning fork . The ratiio of length of pipe A to that of B is
View SolutionAn organ pipe P1 closed at one vibrating in its first overtone and another pipe P2. Open at both ends vibrating in third overtone are in resonance with a given tuning fork. The ratio of the length of P1 to that of P2 is
View SolutionAn organ pipe of length L open at both ends is found to vibrate in its harmonic when sounded with a tuning fork of 480Hz. What should be the length of a pipe closed at one end, so that it also vibrates in its first harmonic with the same tuning fork?
View SolutionAn organ pipe P closed at one end vibrates in its first
narmonic. Another organ pipe Q open at both ends
vibrates in its third harmonic. When both are in
resonance with a tuning fork, the ratio of the length of
P to that of Q is
View SolutionA cylindrical pipe of length 29.5cm closed at one end is found to be in resonance when a tuning fork of frequency 864Hz is sounded near the open end. Then the mode of vibration of the air in the pipe is (Velocity of sound in air is 340m/s.)
View SolutionAn organ pipe A closed at one ends is allowed to vibrate in its first harmonic and another pipe B open at both ends is allowed to vibrate in its third harmonic. Both A and B are in resonance with a given tuning fork. The ratio of the length of A and B is
View SolutionAn organ pipe P_(1) closed at one end vibrating in its first harmonic and another pipe P_(2) open at both ends vibrating in its third harmonic are in resonance with a given tuning fork. The ratio of the length of P_(1) to that of P_(2) is-
View SolutionAn organ pipe A closed at one ends is allowed to vibrate in its first harmonic and another pipe B open at both ends is allowed to vibrate in its third harmonic. Both A and B are in resonance with a given tuning fork. The ratio of the length of A and B is
View SolutionAn organ pipe A closed at one ends is allowed to vibrate in its first harmonic and another pipe B open at both ends is allowed to vibrate in its third harmonic. Both A and B are in resonance with a given tuning fork. The ratio of the length of A and B is
View SolutionAn organ pipe A closed at one ends is allowed to vibrate in its first harmonic and another pipe B open at both ends is allowed to vibrate in its third harmonic. Both A and B are in resonance with a given tuning fork. The ratio of the length of A and B is
View SolutionAn organ pipe P_1 closed at one end and vibrating in its first overtone, and another pipe P_2 open at both ends and vibrating in its third overtone, are in resonance with a given tuning fork. The ratio of the length of P_1 to that of P_2 is
View Solution
