Assertion : Displacement-time equation of two particles moving in a straight line are, s1=2t−4t2 and s2=−2t+4t2. Relative velocity between the two will go on increasing.
Reason : If velocity and acceleration are of same sign then speed will increase.
If the both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:D
v1=ds1dt=(2−8t)
v2=ds2dt=(−2+8t)
∴v12=v1−v2=(4−16t)
v12 does not keep on incresing.
Similar Questions
Knowledge Check
Velocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
A12mB16mC4mD8mThe equation of a particle moving along a straight line is s=2t3–9t2+12t, where the units of s and t are cm and s. the acceleration of the particle will be zero after
A32 sB23sC12sD1sThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
A2m/s2B4m/s2C6m/s2D8m/s2
Velocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
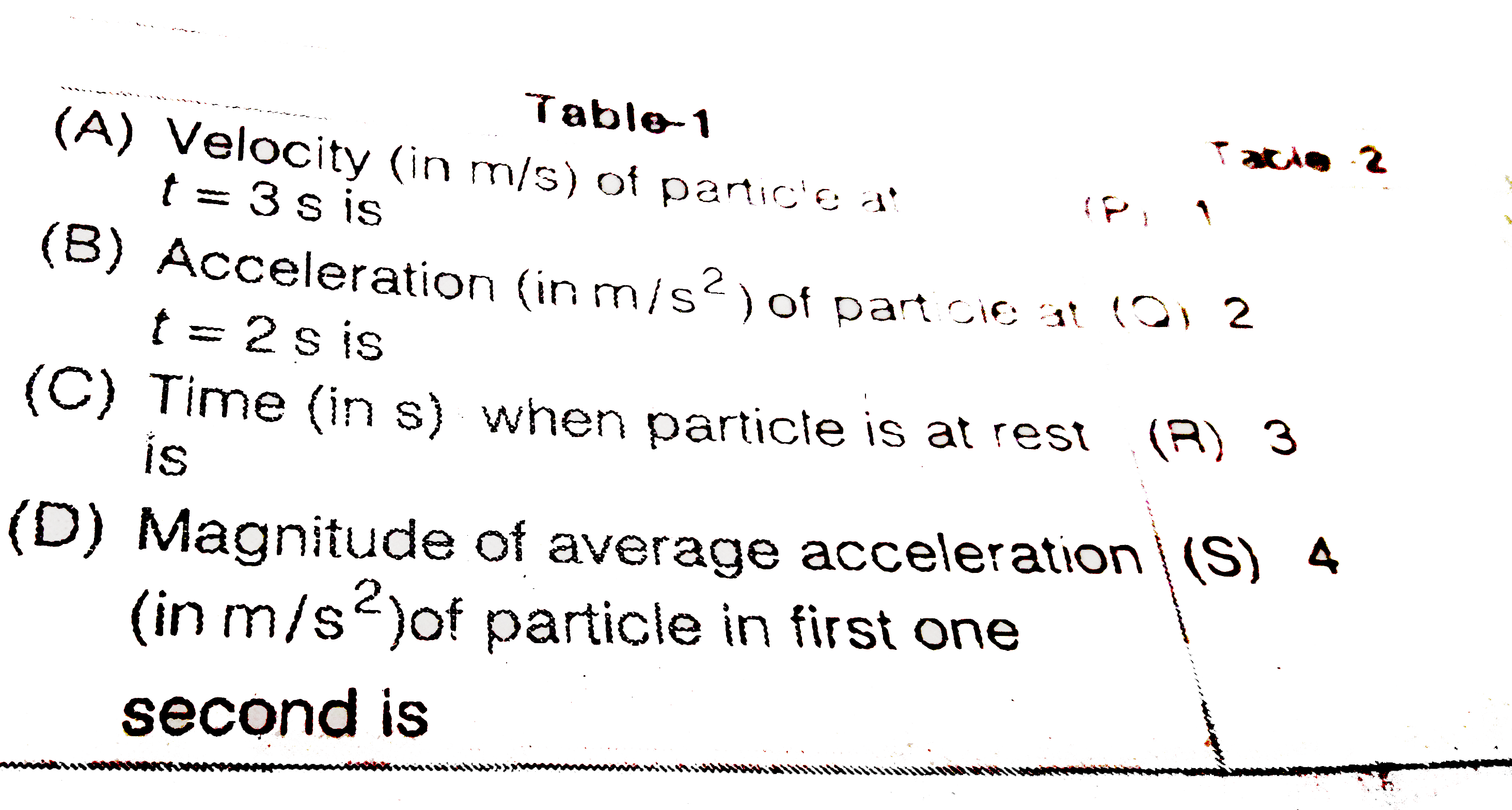
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.

View SolutionThe acceleration of a particle, moving in a straight line, at time t is (2t+1)m/sec2 . If 4m/sec is the initial velocity of the particle then its velocity after 2 sec. is
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
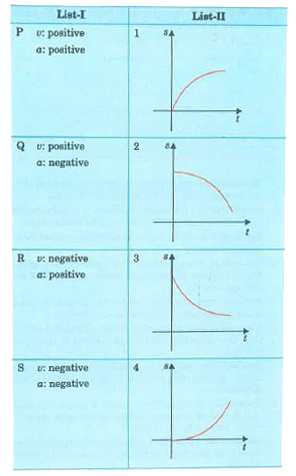
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View Solution

