Assertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
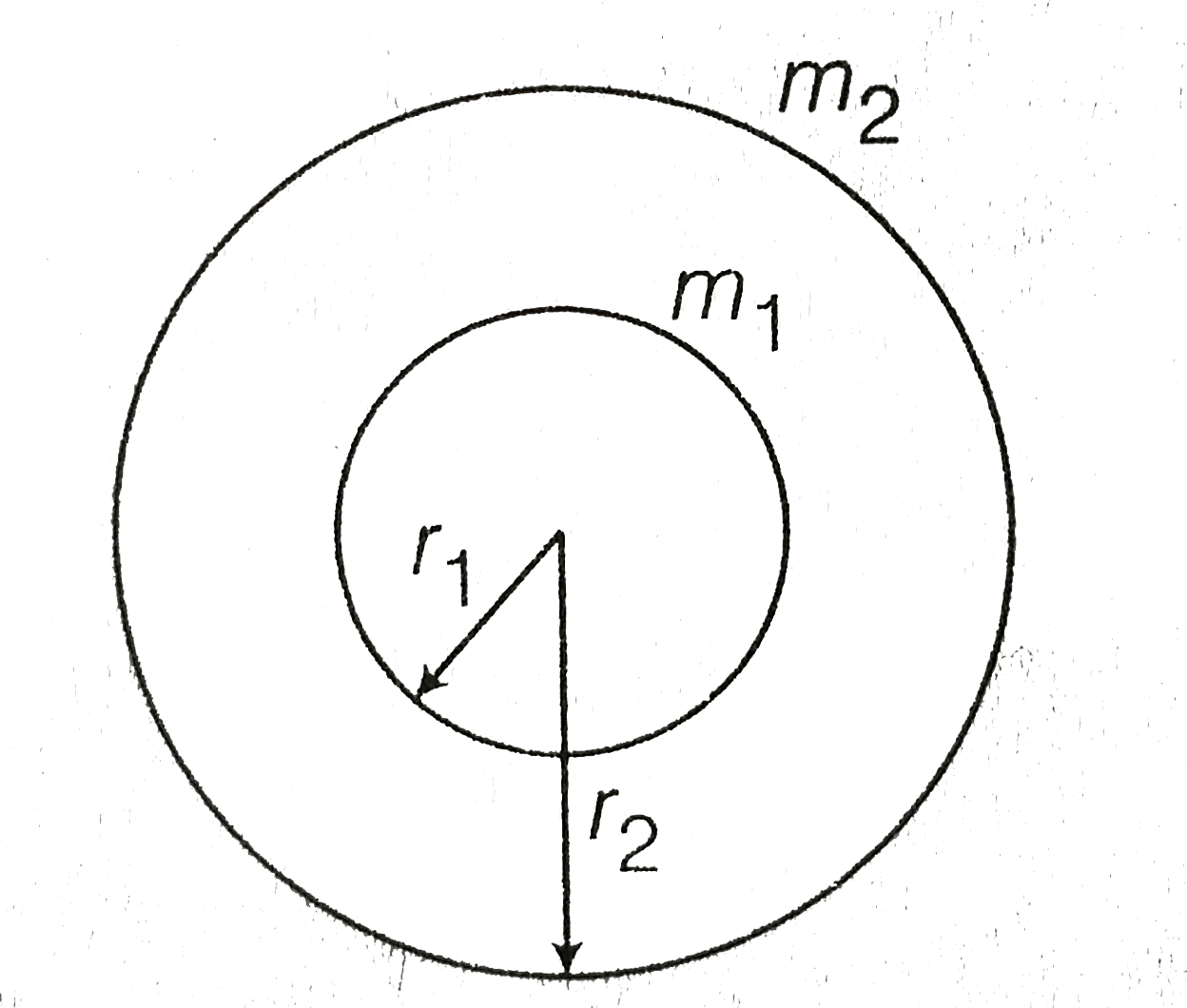
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
If both Assertin and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:D
In the region 0<r<r1
F = 0 but v = constant.
টপার এই প্রশ্নগুলো সমাধান করেছে
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
সম্পর্কিত প্রশ্ন
Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionWeightlessness in satellite is due to
View SolutionIf the dimensions of B2l2C are [MaLbTc], then the value of a+b+c is
[Here B,l and C represent the magnitude of magnetic field, length and capacitance respectively]
View SolutionA particle is projected with velocity 2(√gh), so that it just clears two walls of equal height h which are at a distance of 2h form each other. Show that the time of passing between the walls is 2(√hg). [Hint : First find velocity at height h. Treat it as initial velocity and 2h as the range. ]
View SolutionThe figure represents two concentric shells of radii R_(1) and R_(2) and masses M_(1) and M_(2) respectively. The gravitational field intensity at the point A at distance a (R_(1) lt a lt R_(2)) is
View SolutionTwo concentric spherical shells have masses m1, m2 and radit R1,R2(R1<R2). Calculate the force by this system on a particle of mass m, if it is placed at a distance (R1+R2)2 from the centre.
View SolutionTwo bodies of masses M_(1) and M_(2) , are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionTwo concentric spherical shells have masses m_(1) and m_(2) and radii r_(1) and r_(2) (r_(2) gt r_(1)) . What is the force exerted by this system on a particle of mass m_(3) . If it is placed at a distance r(r_(1) lt r lt r_(2)) from the centre ?
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1

Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionTwo concentric spherical shells of masses and radii m_(1), r_(1) and m_(2), r_(2) respectively are as shown. The gravitational field intensity at point P is
View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
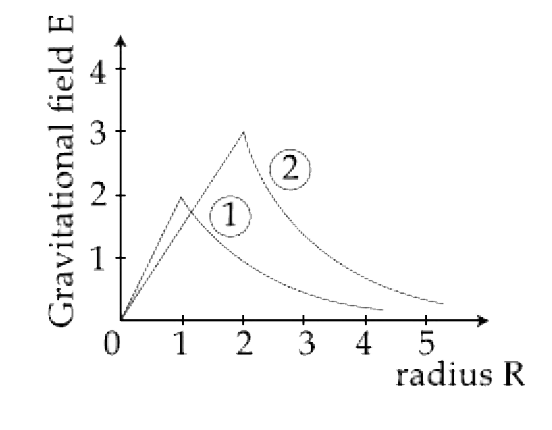
View SolutionTwo concentric spherical shells have masses M1,M2 and radii R1,R2(R1<R2). The force exerted by this system on a particle of mass m. If it is placed at a distance (R1+R22) from the centre.
View SolutionTwo concentric spherical shells have masses M_(1), M_(2) and radii R_(1), R_(2)(R_(1) lt R_(2)) . The force exerted by this system on a particle of mass m. If it is placed at a distance ((R_(1)+R_(2))/(2)) from the centre.
View SolutionThe figure represents two concentric shells of radii R_(1) and R_(2) and masses M_(1) and M_(2) respectively. The gravitational field intensity at the point A at distance a (R_(1) lt a lt R_(2)) is
View SolutionTwo concentric spherical shells have masses m1, m2 and radit R1,R2(R1<R2). Calculate the force by this system on a particle of mass m, if it is placed at a distance (R1+R2)2 from the centre.
View Solution

