Assuming the Sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant powered incident of Earth at a distance r from the sun
where r0 is the radius of the Earth and σ is Stefan's constant.
4πr20R2σT4/r2
πr20R(2)σT4/r2
r20R2σT4/4πr2
R2σT4/r2
(b)
Similar Questions
Assuming the sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant power, incident on earth, at a distance 'r' from the sun (where r0 is the radius of the earth and σ is stefan's constant)
View SolutionIf the temperature of sun were to increase from T to 2T and its radius from R to 2 R, then ratio of radiant energy received on earth to what it was previously will be
View SolutionAssuming the sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant power, incident on earth, at a distance 'r' from the sun (where r0 is the radius of the earth and σ is stefan's constant)
View SolutionAssuming the sun to have a spherical outer surface of radius r radiating like a black body at temperature t∘C. The power received by a unit surface (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
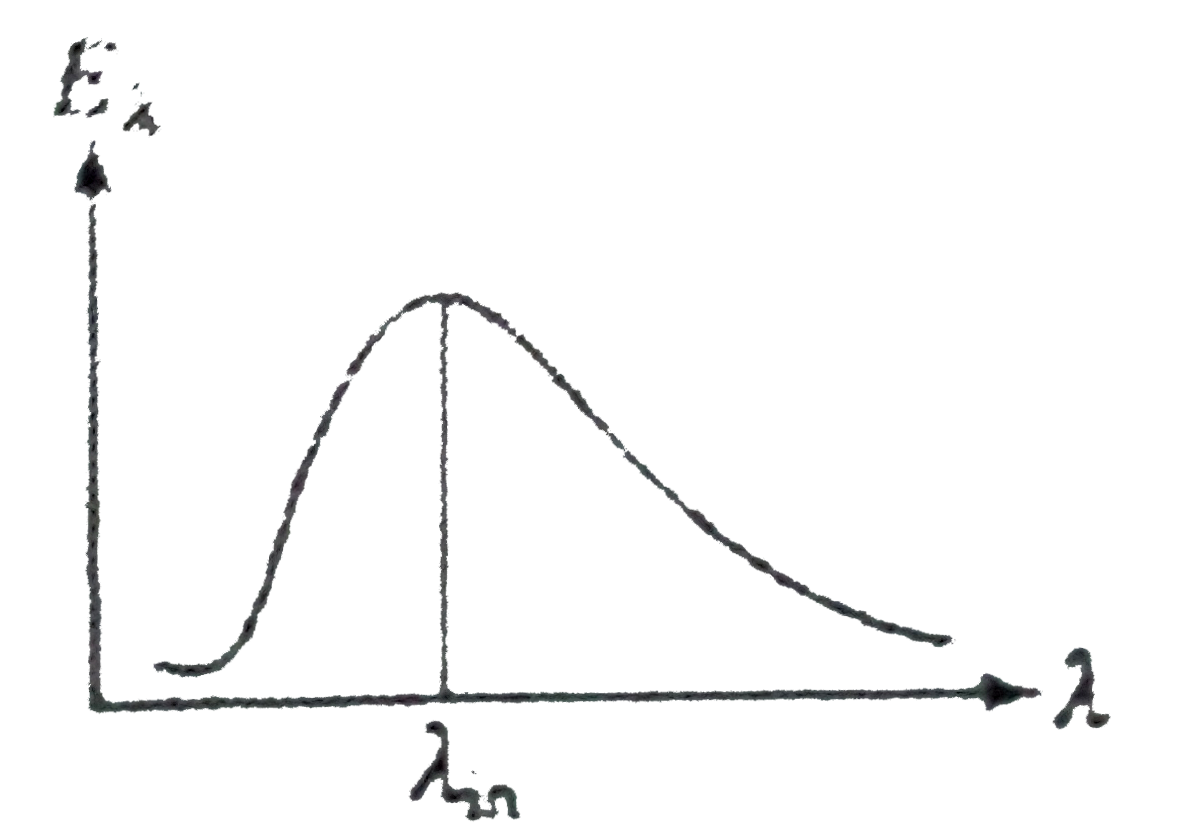
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionAssuming the Sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant powered incident of Earth at a distance r from the sun where r_0 is the radius of the Earth and sigma is Stefan's constant.
View SolutionAssuming the Sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant powered incident of Earth at a distance r from the sun
where r0 is the radius of the Earth and σ is Stefan's constant.
View SolutionR_(s), d And R_(e ) The radius of the Sun, the center of the Sun and the radius of the Earth are respectively. If the temperature of the Sun is T, then the total amount of radiation incident on the earth is
View Solution

