At t=0,a transverse wave pulse travelling in the positive x direction with a speed of 2m/s in a wire is described by the function y=6/x2 given that x≠0. Transverse velocity of a particle at x=2 m and t= 2 s is
3m/s
−3m/s
8m/s
−8m/s
The correct Answer is:b
To solve the problem step by step, we will follow the process outlined in the video transcript.
Step 1: Understand the wave equation
The wave pulse is described by the function y=6x2 at t=0. The wave travels in the positive x-direction with a speed of v=2m/s.
Step 2: Write the general wave equation
The general form of a wave pulse traveling in the positive x-direction is given by:
y(x,t)=A(x−vt)2
where A is a constant, v is the speed of the wave, x is the position, and t is the time.
Given that at t=0, y=6x2, we can identify A=6 and write the wave equation as:
y(x,t)=6(x−vt)2
Step 3: Substitute the speed of the wave
Substituting v=2m/s into the equation gives:
y(x,t)=6(x−2t)2
Step 4: Find the transverse velocity
The transverse velocity (particle velocity) is given by:
vp=∂y∂t
To find this, we need to differentiate y with respect to t.
Step 5: Differentiate the wave equation
Using the chain rule, we differentiate y:
y=6(x−2t)−2
Differentiating with respect to t:
∂y∂t=6⋅(−2)⋅(x−2t)−3⋅(−2)=−24(x−2t)3
Step 6: Substitute x=2m and t=2s
Now we substitute x=2 and t=2 into the equation:
vp=−24(2−2⋅2)3=−24(2−4)3=−24(−2)3=−24−8=3m/s
Final Answer
The transverse velocity of the particle at x=2m and t=2s is:
vp=−3m/s
The wave pulse is described by the function y=6x2 at t=0. The wave travels in the positive x-direction with a speed of v=2m/s.
The general form of a wave pulse traveling in the positive x-direction is given by:
y(x,t)=A(x−vt)2
where A is a constant, v is the speed of the wave, x is the position, and t is the time.
y(x,t)=6(x−vt)2
Substituting v=2m/s into the equation gives:
y(x,t)=6(x−2t)2
The transverse velocity (particle velocity) is given by:
vp=∂y∂t
To find this, we need to differentiate y with respect to t.
Using the chain rule, we differentiate y:
y=6(x−2t)−2
Differentiating with respect to t:
∂y∂t=6⋅(−2)⋅(x−2t)−3⋅(−2)=−24(x−2t)3
Now we substitute x=2 and t=2 into the equation:
vp=−24(2−2⋅2)3=−24(2−4)3=−24(−2)3=−24−8=3m/s
The transverse velocity of the particle at x=2m and t=2s is:
vp=−3m/s
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Single Correct Answer
Explore 1 Video
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Multiple Correct
Explore 25 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Subjective
Explore 16 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICS ENGLISHChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The figure shows three progressive waves A, B and c. wahat canbe concluded from the figure that with respect to wave A?
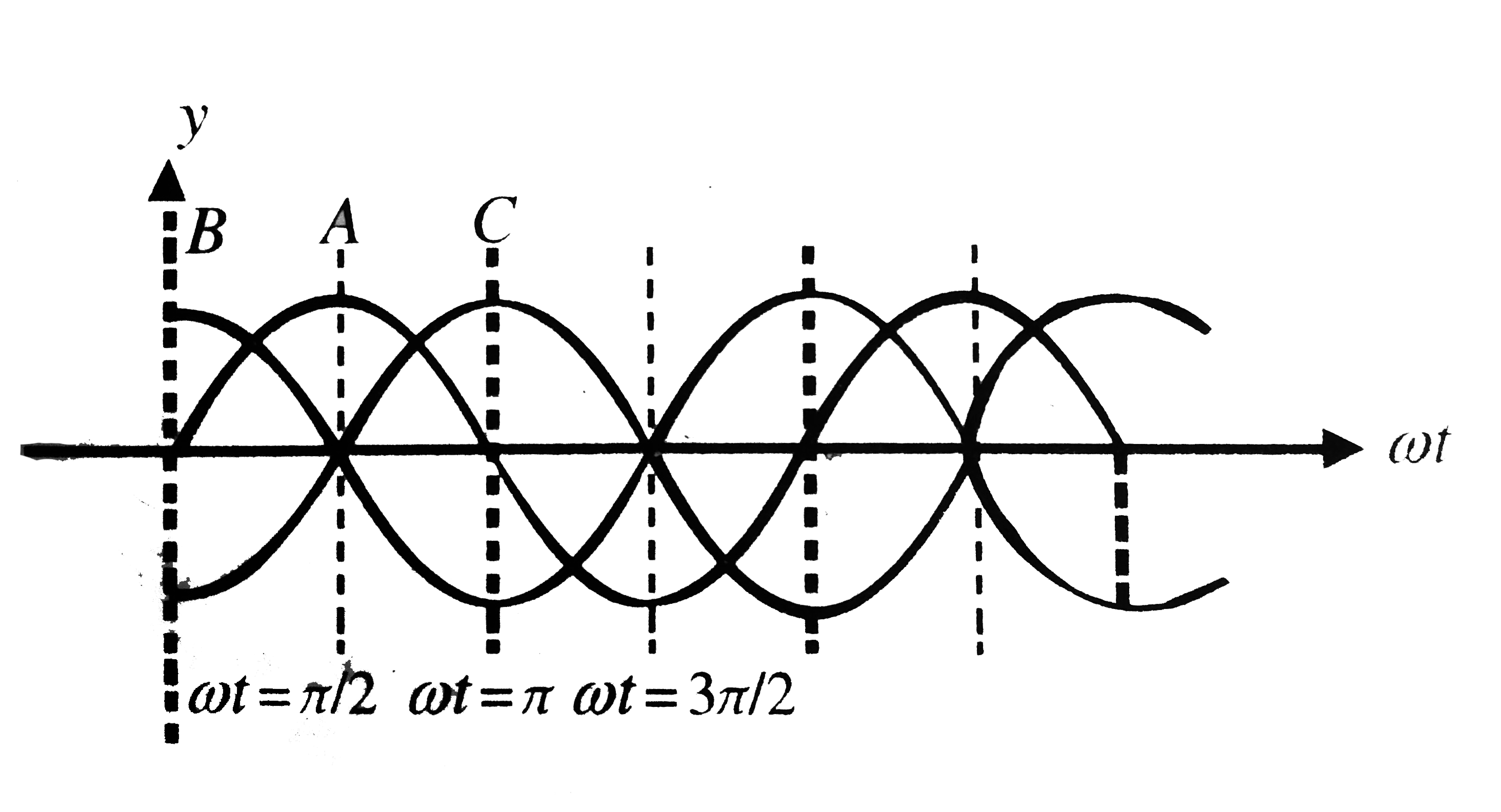
View SolutionA wave equation which gives the displacement along the y-direction is given by y=10−4sin(60t+2x) where xandy are in meters and t is time in seconds. This represents a wave
View SolutionA 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionIf at t=0, a travelling wave pulse in a string is described by the function,
y=10(x2+2)
Hence, xandy are in meter and t in second. What will be the wave function representing the pulse at time t, if the pulse is propagating along positive x-axix with speed 2m/s?
View SolutionAt t=0, transverse pulse in a wire is described by the function
y=6x2+3
where x and y are in metres. Write the function y(x,t) that describe this plus if it is travelling in the positive x-direction with a speed of 4.50m/s.
View SolutionAt t=0,a transverse wave pulse travelling in the positive x direction with a speed of 2m/s in a wire is described by the function y=6/x2 given that x≠0. Transverse velocity of a particle at x=2 m and t= 2 s is
View SolutionAt t=0, a transverse wave pulse in a wire is described by the function y=6//(x^(2)-3) where x and y are in metres. The function y(x,t) that describes this wave equation if it is travelling in the positive x direction with a speed of 4.5 m//s is
View SolutionA hypothetical pulse is travelling along positive x direction on a taut string. The speed of the pulse is 10cms–1. The shape of the pulse at t = 0 is given as
y=x6+1for−6<x≤0=−x+1for0≤x<1=0for all other values of x
x and y are in cm.
(a) Find the vertical displacement of the particle at x = 1 cm at t = 0.2 s
(b) Find the transverse velocity of the particle at x = 1 cm at t = 0.2 s.
View SolutionA transverse wave of frequency 500 Hz and speed 100 m/s is traveling in the positive x direction on a long string. At time t = 0 s the displacements at x = 0.0 m and at x = 0.25 m are 0.0 m and 0.02 m, respectively. The displacement at x = 0.2 m at t = 5xx10^(-4) s is
View SolutionAt t = 0 , a transverse wave pluse in a wire is described by the funcation y = (6)/(x^(3) + 3) where x and y are in meters write the funcation y(x, t) that describes this wave if it is travelling in the positive x direction with a speed of 4.5 m//s .
View SolutionA wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by y=2/(t^2+1) Find (i) Expression of the function y = (x, t) i.e., displacement of a particle position x and time t.
View SolutionAt t=0 , a transverse were pulse in a wire is described by the function where x and y are in metre. The function y(x, t) that describes this wave equation, if it is travelling in the positive x - direction with a speed of "4.5 m s"^(-1) is
View SolutionAt t = 0 a travelling wave pulse on a string is described by the function y=10x2+2 , here x and y are in meter and t in second. What will be the wave function representing the pulse at time t, if the pulse is propagating along the positive x-axis with speed 2m/s ?
View SolutionAt t = 0 a travelling wave pulse on a string is described by the function y=10/(x^(2) +2) , here x and y are in meter and t in second, What will be the wave function representing the pulse at time t. if the pulse is propagating along ihe positive x-axis with .speed 2m/s .?
View Solution
