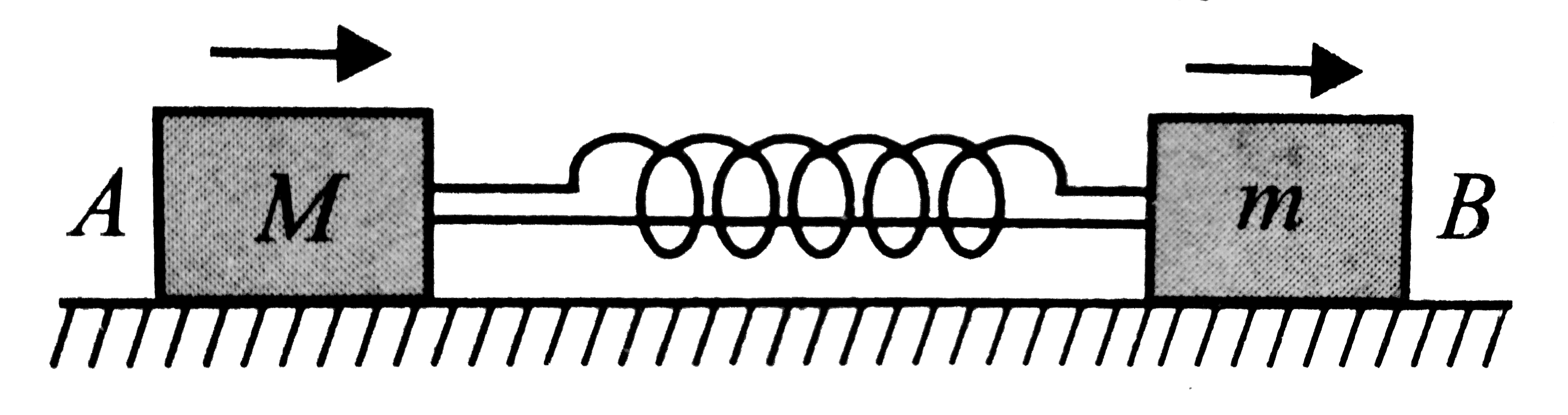
Block A of massM=2kg is connected to another block B of mass m=1kg with a string and a spring of force constant k=600N/m as shown in Fig. Initially, spring is compressed to 10cm and whole system is moving on a smooth surface with a velocity v=1m/s. At any time, thread is burnt, the velocity of block A, when B is having maximum velocity w.r.t. ground, is
zero
1m/S
3m/s
none of these
The correct Answer is:C
The velocity of B will be maximum when spring comes to its natural length. Let at the at time their velocities are v1 and v2 as shown

Conservation of momentum,
2v1+1v2(2+1)×1⇒2v1+v2=3…..i
Conservation of energy
122v21+121v22=12600(10100)2=123(1)2⇒2v21+v22=9
From eqn i and ii
v1=2m/s,v2=−1m/s or v1=0,v2=3m/s
The second solution is possible.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.
View SolutionTwo identical smooth balls are projected from points O and A on the horizontal ground with same speed of projection. The angle of projection in each case is 30∘.The distance between O and A is 100m. The balls collide in mid-air and return to their respective points of projection. If the coefficient of restitution is 0.7, find the speed of projection of either ball (in m/s) correct to nearest integer. (Take g=10ms−2 and √3=1.7)
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionBlock A of massM=2kg is connected to another block B of mass m=1kg with a string and a spring of force constant k=600N/m as shown in Fig. Initially, spring is compressed to 10cm and whole system is moving on a smooth surface with a velocity v=1m/s. At any time, thread is burnt, the velocity of block A, when B is having maximum velocity w.r.t. ground, is

View SolutionA block of mass m = 25 kg on a smooth horizontal surface with a velocity vec v = 3 ms^(-1) meets the spring of spring constant k = 100 N//m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are. .
View SolutionTwo blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is

View SolutionTwo blocks of masses m = 2 kg and m = 8 kg are connected to a spring of force constant K = 1 kN//m . The spring is compressed by 20 cm and the two blocks are held in this position by a string. The system is placed on a horizontal smooth surface and given a velocity u = 3 m//s perpendicular to the spring. The string snaps while moving. Find the speed of the block of mass m when the spring regains its natural length.
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View Solution

