Consider a capacitor charging circuit. Let Q1 be the charge given to the capacitor in time interval of 20ms and Q2 be the charge given in the next time interval of 20ms. Let 10μC charge be deposited in a time interval t1 and the next 10μC charges is deposited in the next time interval t2. Then
Q1>Q2,t1>t2
Q1>Q2,t1<t2
Q1<Q2,t1>t2
Q1<Q2,t1<t2
The correct Answer is:B
Step-by-Step Solution:
1. Understanding the Charging of a Capacitor:
- When a capacitor is connected to a voltage source, it charges up over time. The rate of charging is not constant; it starts off quickly and slows down as the capacitor approaches its maximum charge.
2. Defining the Charges:
- Let Q1 be the charge deposited in the first time interval t1=20ms.
- Let Q2 be the charge deposited in the next time interval t2=20ms.
- According to the problem, Q1=10μC and Q2=10μC as well.
3. Analyzing the Charging Behavior:
- Initially, the capacitor charges rapidly, meaning that during the first time interval t1, the capacitor receives a significant amount of charge quickly.
- As time progresses and the capacitor charges, the rate of charge deposition decreases, leading to a longer time required to deposit the same amount of charge.
4. Comparing Charges and Time Intervals:
- Since the first charge Q1 is deposited quickly, it can be inferred that Q1>Q2 because the second charge Q2 takes longer to deposit due to the slowing rate of charging.
- Therefore, t1<t2 since it takes more time to deposit the same amount of charge as the capacitor approaches its maximum charge.
5. Conclusion:
- From the analysis, we conclude that:
- Q1>Q2
- t1<t2
Final Result:
- The correct options are:
- Q1 is greater than Q2
- t1 is less than t2
- When a capacitor is connected to a voltage source, it charges up over time. The rate of charging is not constant; it starts off quickly and slows down as the capacitor approaches its maximum charge.
- Let Q1 be the charge deposited in the first time interval t1=20ms.
- Let Q2 be the charge deposited in the next time interval t2=20ms.
- According to the problem, Q1=10μC and Q2=10μC as well.
- Initially, the capacitor charges rapidly, meaning that during the first time interval t1, the capacitor receives a significant amount of charge quickly.
- As time progresses and the capacitor charges, the rate of charge deposition decreases, leading to a longer time required to deposit the same amount of charge.
- Since the first charge Q1 is deposited quickly, it can be inferred that Q1>Q2 because the second charge Q2 takes longer to deposit due to the slowing rate of charging.
- Therefore, t1<t2 since it takes more time to deposit the same amount of charge as the capacitor approaches its maximum charge.
- From the analysis, we conclude that:
- Q1>Q2
- t1<t2
- The correct options are:
- Q1 is greater than Q2
- t1 is less than t2
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
In the circuit shown as potential difference of 60V is appliled across AB. The potential difference between the points M and N is
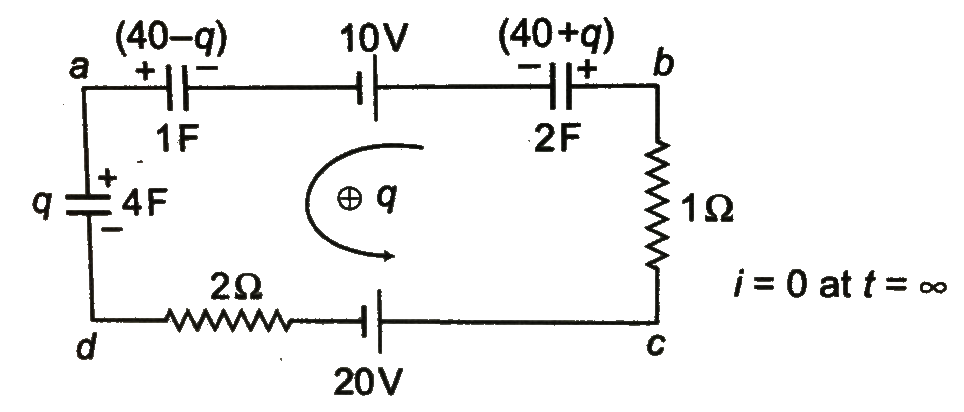
View SolutionIn the circuit shown as potential difference of 60V is appliled across AB. The potential difference between the points M and N is

View SolutionGiven the value of Rydberg constant is 107m−1, the waves number of the last line of the Balmer series in hydrogen spectrum will be:
View SolutionThe LC product of a tuned amplifier circuit require to generate a carrier wave of 1 MHz for amplitude modulation is
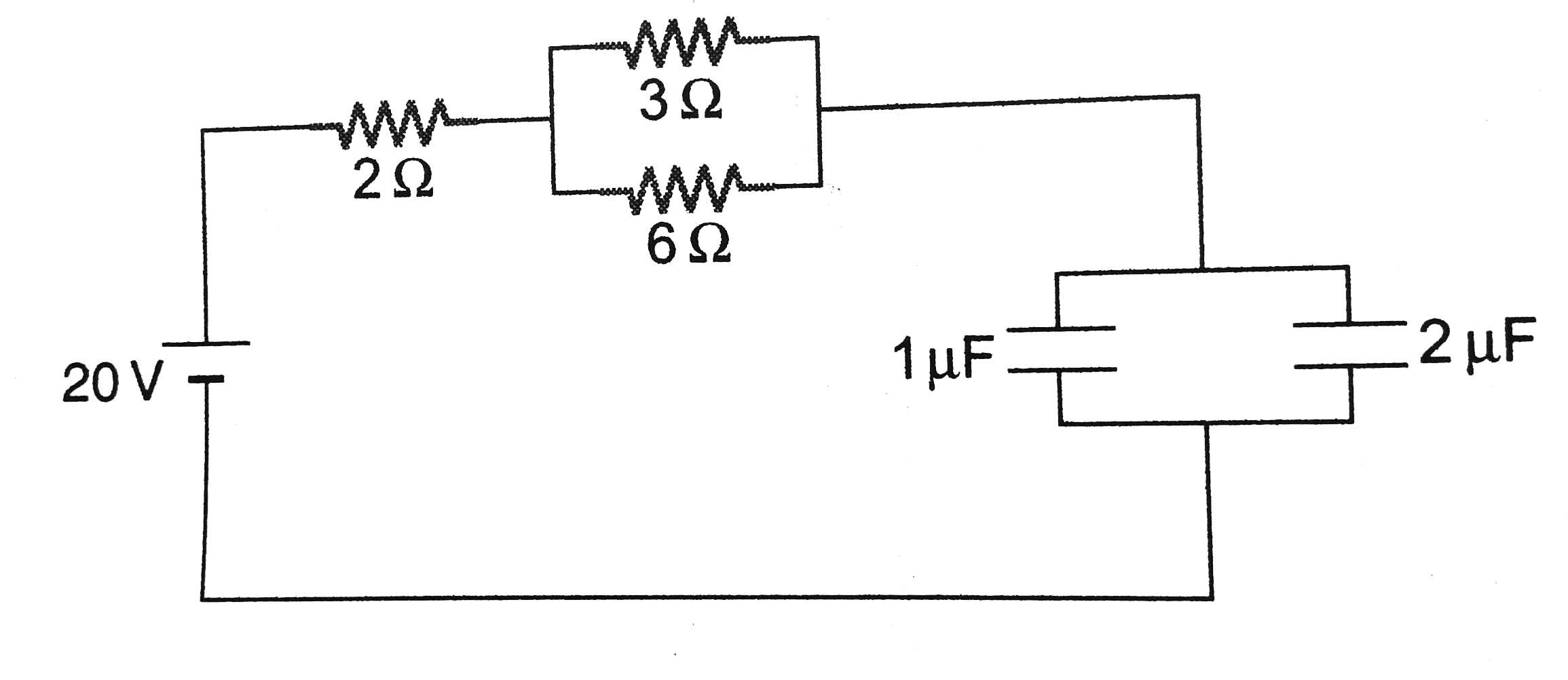
View SolutionThe capacitors are initially uncharged. In a certain time the capacitor of capacitance 2μF gets a charge of 20μC. In that time interval find the heat produced by each resistor individually.
View SolutionIn the given circuit, the capacitor of capacitance C is charged by closing key K at t = 0. Find the time required to charge the capacitor up to the maximum charge for the given circuit, if it were to be charged with the charged with constant initial charging rate at t = 0 in the given circuit.
View SolutionThe charge on 4nuF capacitor in the given circuit is in muC
View SolutionThe time constant of charging of the capacitor charging of the capacitor shown in figure is
View SolutionA circuits contains a capacitor and inductance each with negligible resistance. The capacitor is initially charged and the charging battery is disconnected. At subsequent time , the charge on the capacitor will
View SolutionA circuit contains a capacitor and inductance each with negligible resistance. The capacitor is initially charged and the charging battery is disconnected. At subsequent time, the charge on the capacitor will
View SolutionC1 तथा C2 धारिता के दो संधारित्रों के समांतर संयोजन को Q आवेश दिया जाता है C1 पर Q1 ,C2 पर Q2 आवेश होने पर Q1Q2 का अनुपात होगा---
View SolutionThe charge deposited on 4muF capacitor in the given circuit is:
View SolutionIn the given circuit switch K is open. The charge on the capacitor is C is steady-state is q_1 Now the key is closed and steady-state charge on C is q_2 The ratio of charges q_1//q_2 is -
View SolutionIN A CHARGING R-C CIRCUIT, CHARGE ON A CAPACITOR WITH TIME
View SolutionIN A CHARGING RC CIRCUIT, CHARGE ON A CAPACITOR AFTER 1 TIME CONSTANT IS
View SolutionA charged capacitor and an inductor are connected in series. At time t = 0, the current is zero, but the capacitor is charged. If T is the period of the resulting oscillations, the next time after t = 0, the maximum voltage across the inductor is
View Solution

