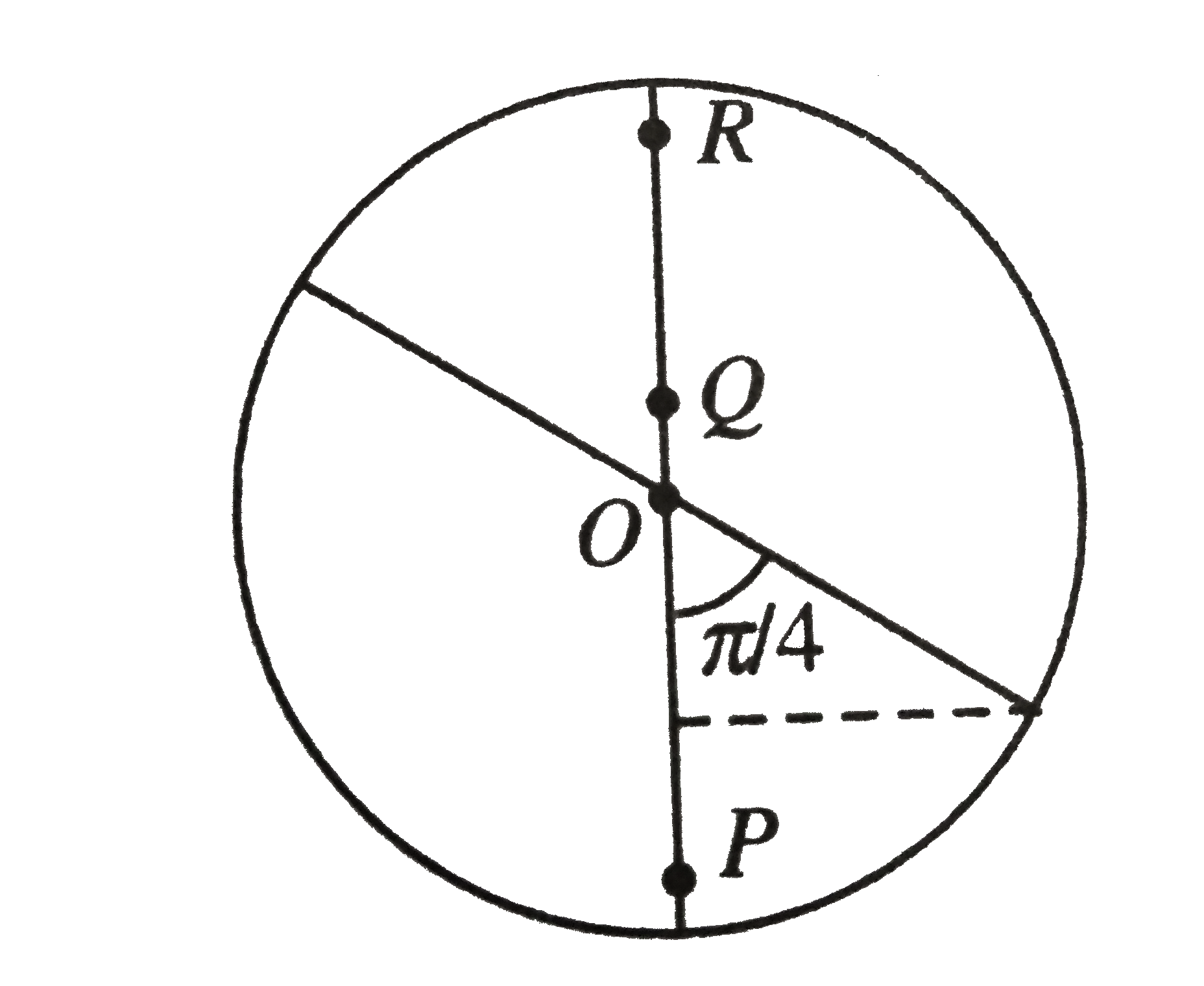
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its center O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 1/8 rotation, (ii) their range is less than half the disc radius, and (iii) ω remains constant throughout. Then
1.png)
P lands in the shaded region and Q in the unshaded region.
P lands in the unshaded region and Q in the shaded region.
Both P and Q land in the unshaded region.
Both P and Q land in the shaded region.
The correct Answer is:C
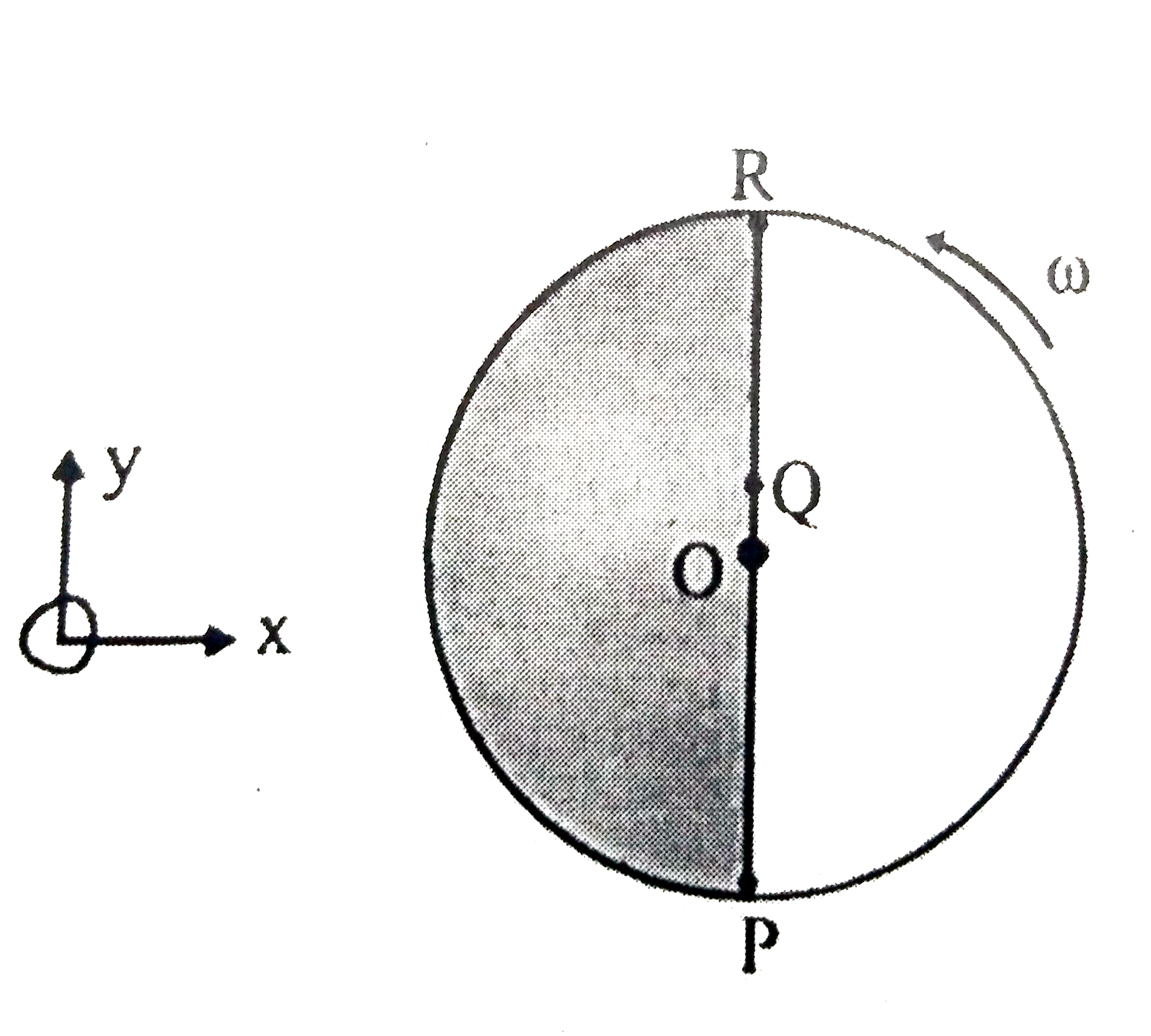
c. At t=18×2πω=π4ω
x-coordinate of P=ωR(π4ω)
=πR4>Rcos45∘
Therefore, both particles P and Q land in unshaded region.
टॉपर्स ने हल किए ये सवाल
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Multiple Correct Answer Type
Explore 24 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Linked Comprehension Type
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
समान प्रश्न
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
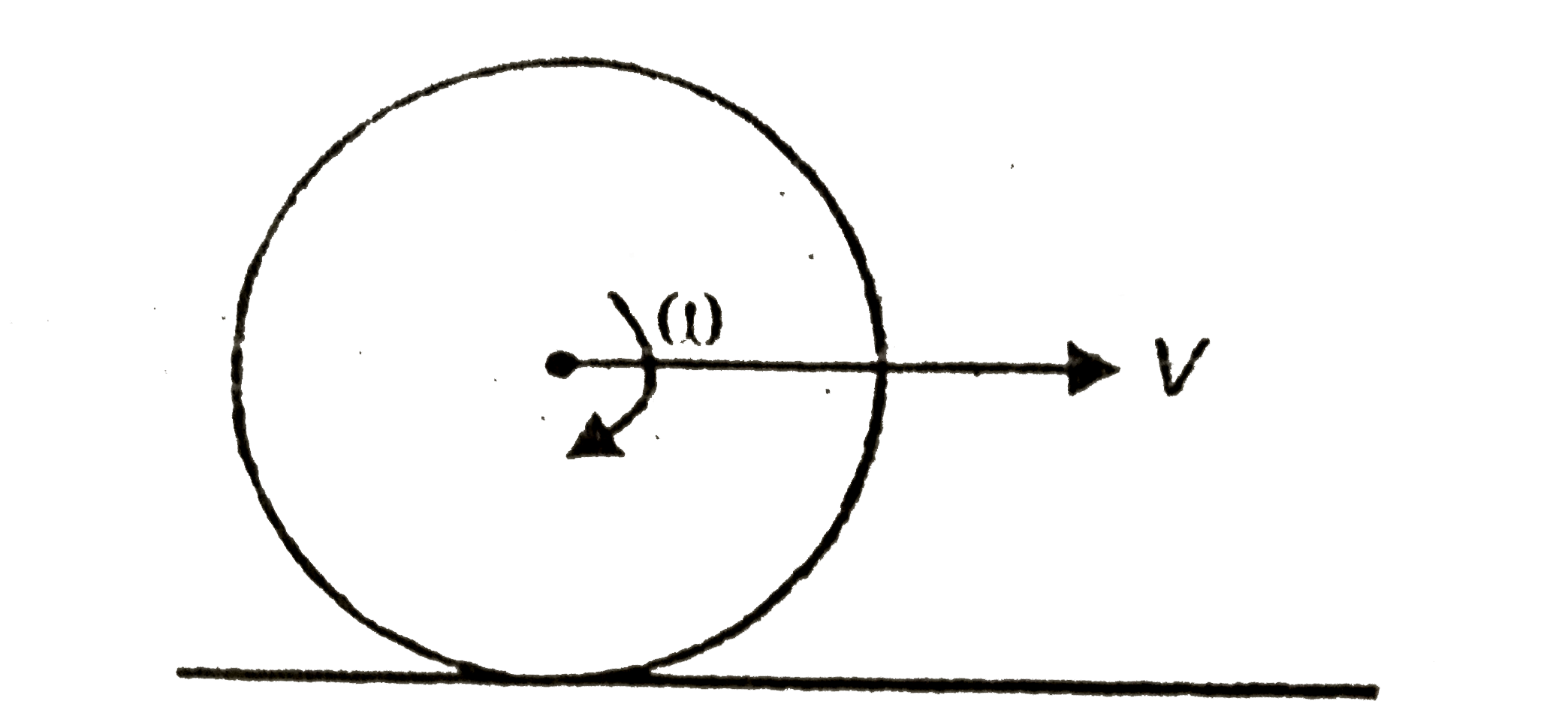
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
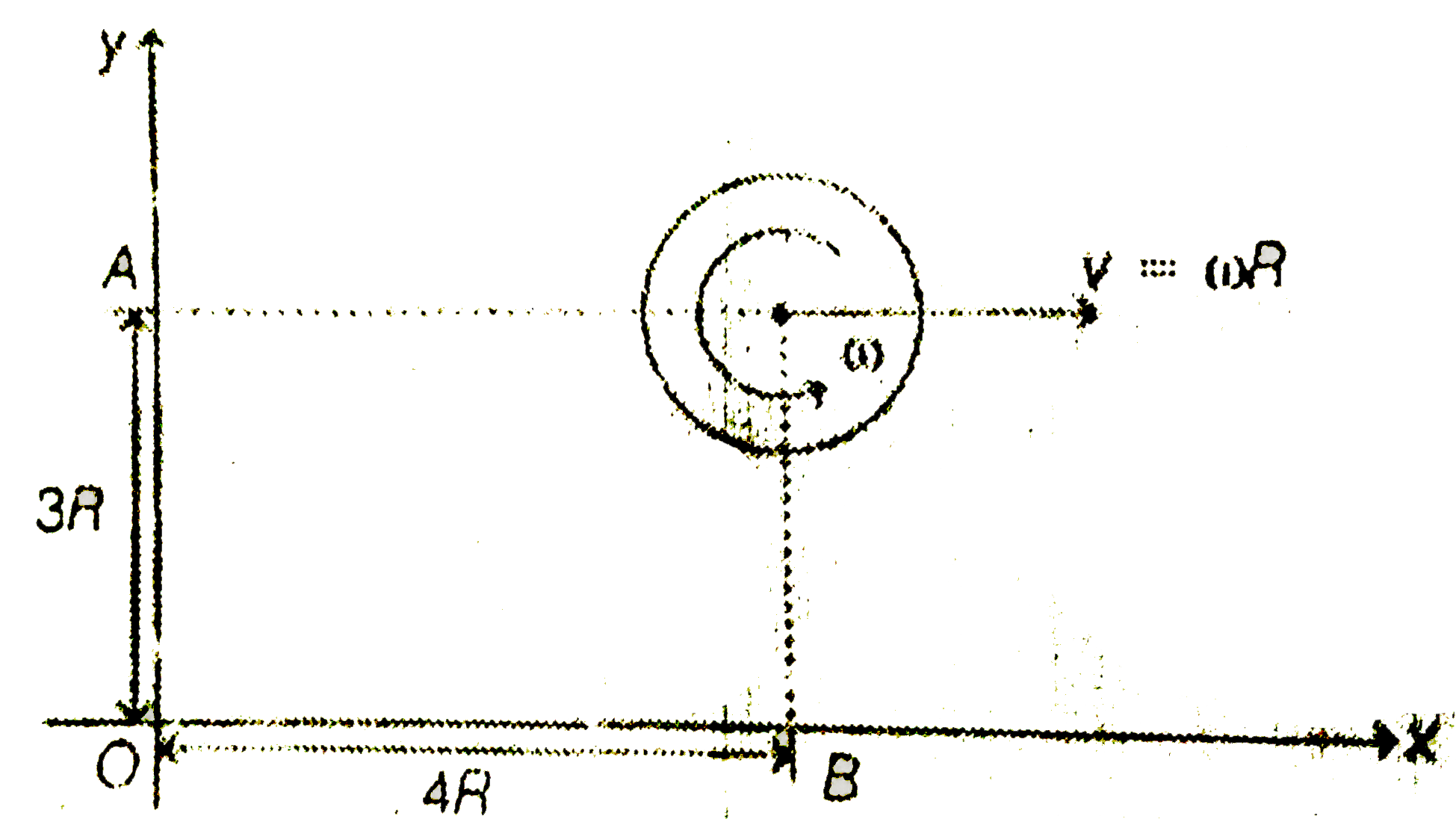
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
View SolutionFind the angular momentum of a disc about the axis shown in figure in the following situations.
View SolutionA metal disc of radius a rotates with a constant angular velocity ω about its axis. The potential difference between the center and the rim of the disc is (m = mass of electron, e = charge on electro)
View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
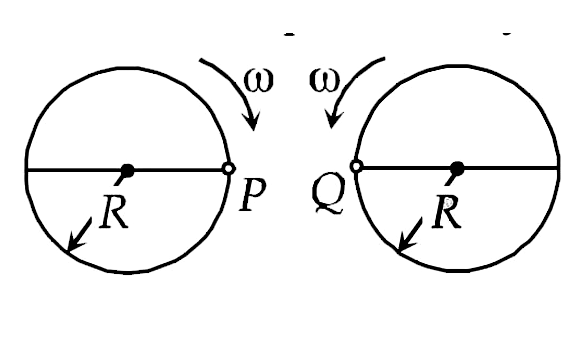
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
