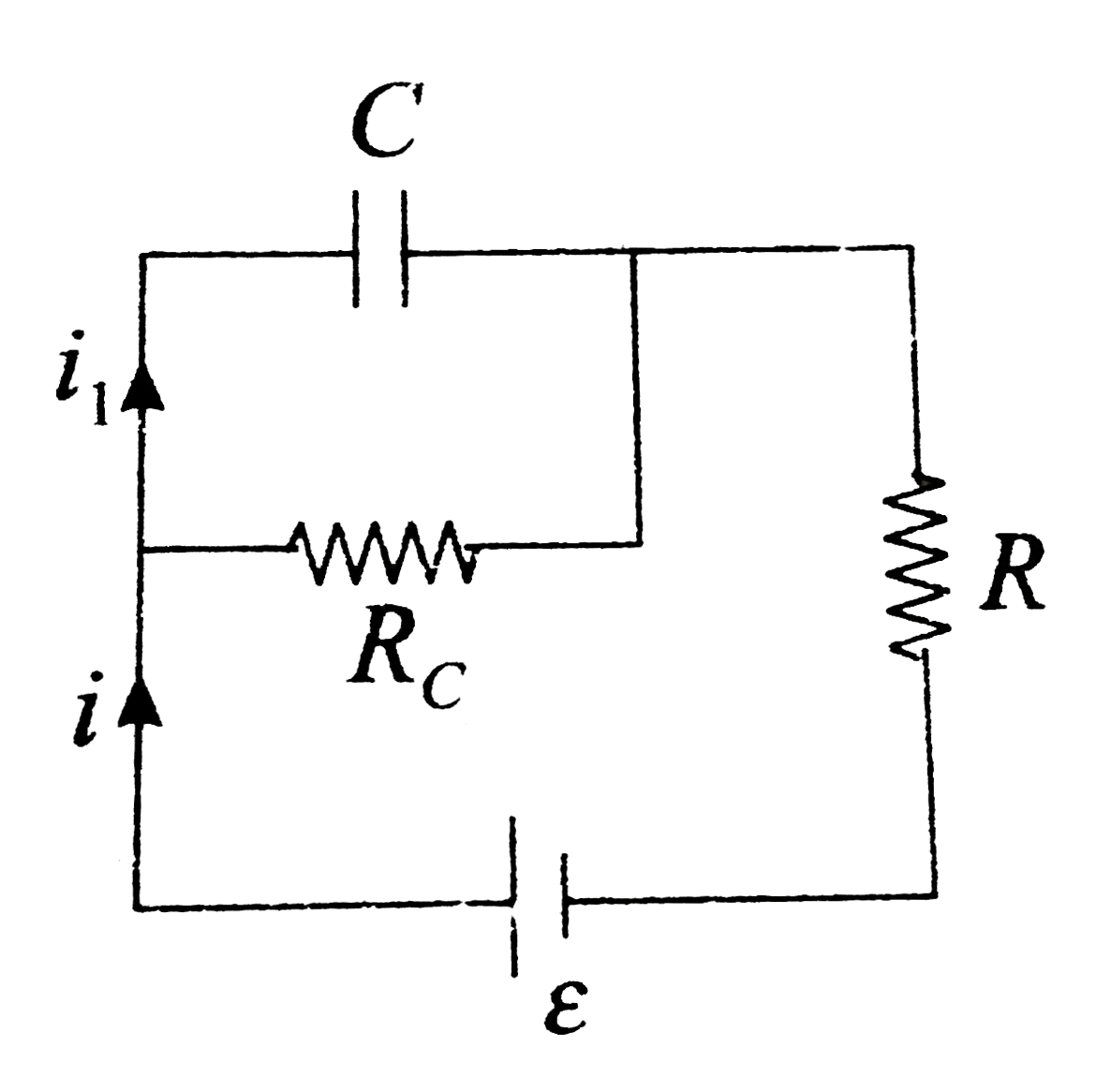
Consider a parallel pate capacitor of capactance C with partially conducting medium between its plates having a resistacne Rc if this capacitor is connected to a battery of emf ε and a resistor R as shown in fig.
a. charge on the capacitor as a function of time.
The switch R as a function of time.

The equivalent circuit can be drawn as shown. Applying
Kirchhoff's law for the two loops,
(i−i1)RC+iR=ε (i)
qC=RC(i=i1) (ii)
Eliminating I between (i) and (ii) we get
qC=(1+RRC)+i1R=ε
For capacitor C,dqdt=i1
dqdt=CE−q(1+α)RC(whereα=RC)
Solving, we get
q=EC1+α(1−e−t(1+α)/RC)
Adding (i) and (ii), we get
QC+iR=Eori=CE−qRC
Substituting for q, we get
I=ER[1−11+α(1−e−t(1+α)RC)](whereα=RRC)
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Single Correct
Explore 72 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Multiple Correct
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.2
Explore 48 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
The switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionFigure shows a LCR circuit connected with a battery emf ε and internal resistance 'R'. After a long time (initially the capacitor was uncharged)

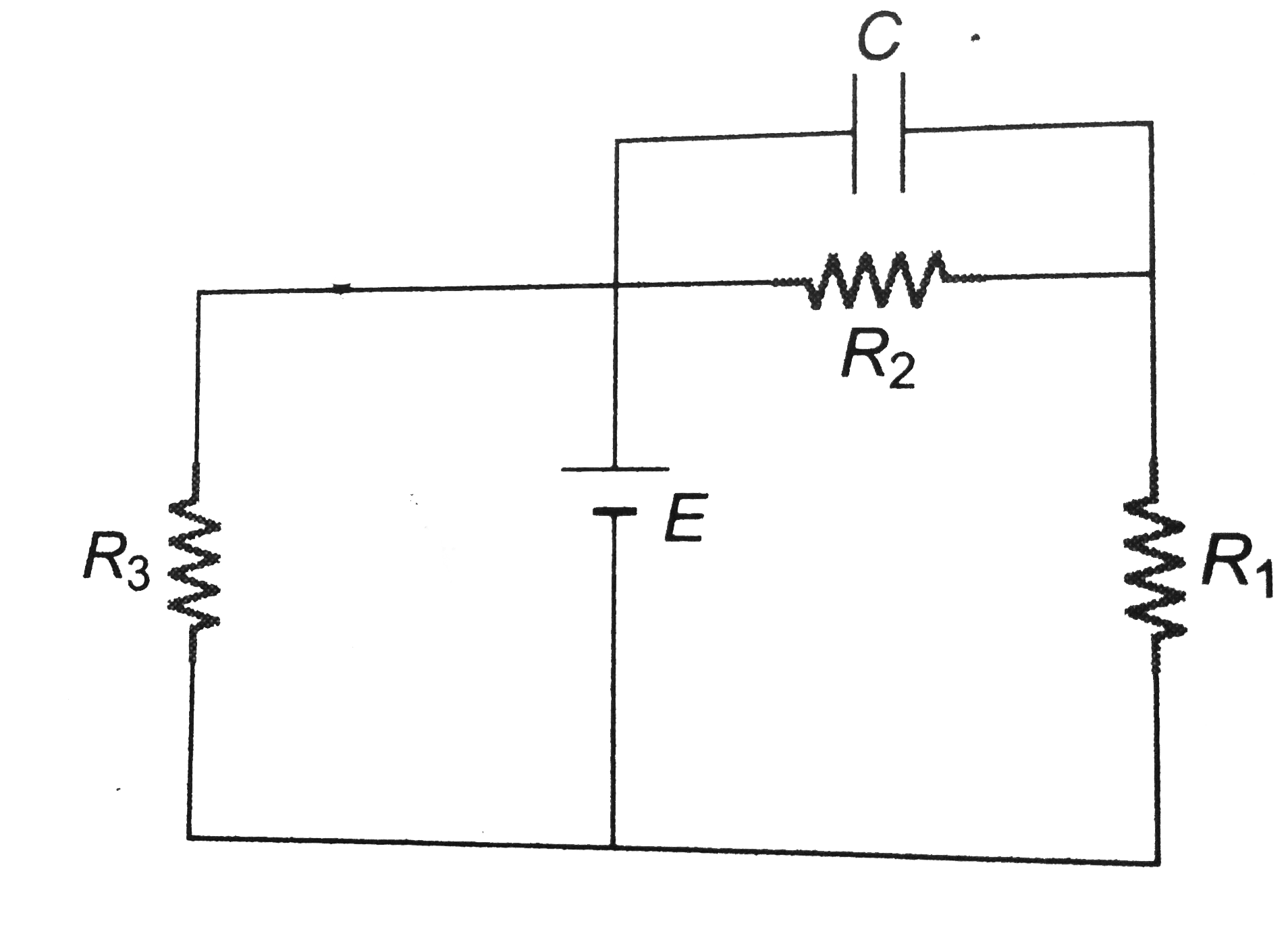
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

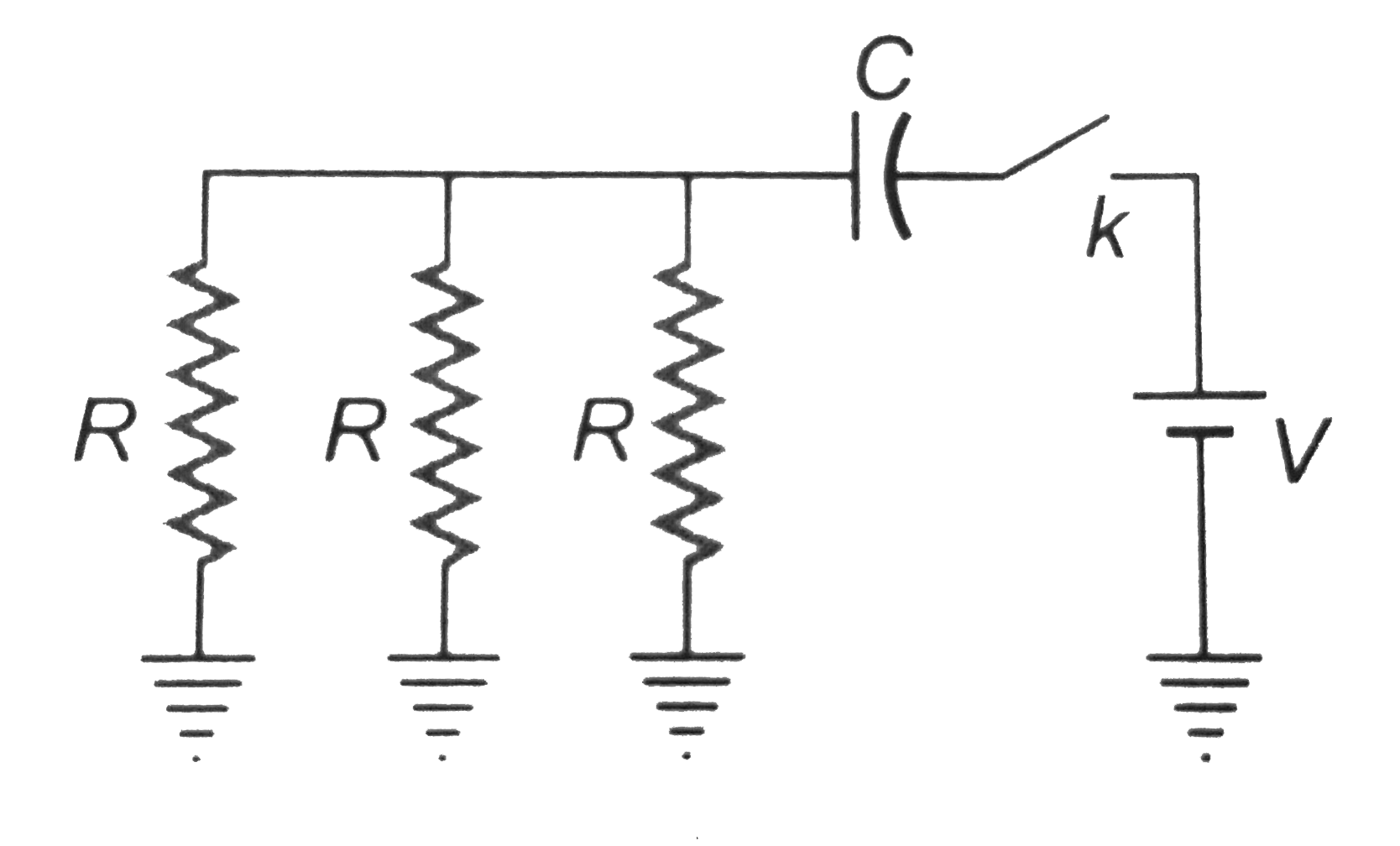
View SolutionThe charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
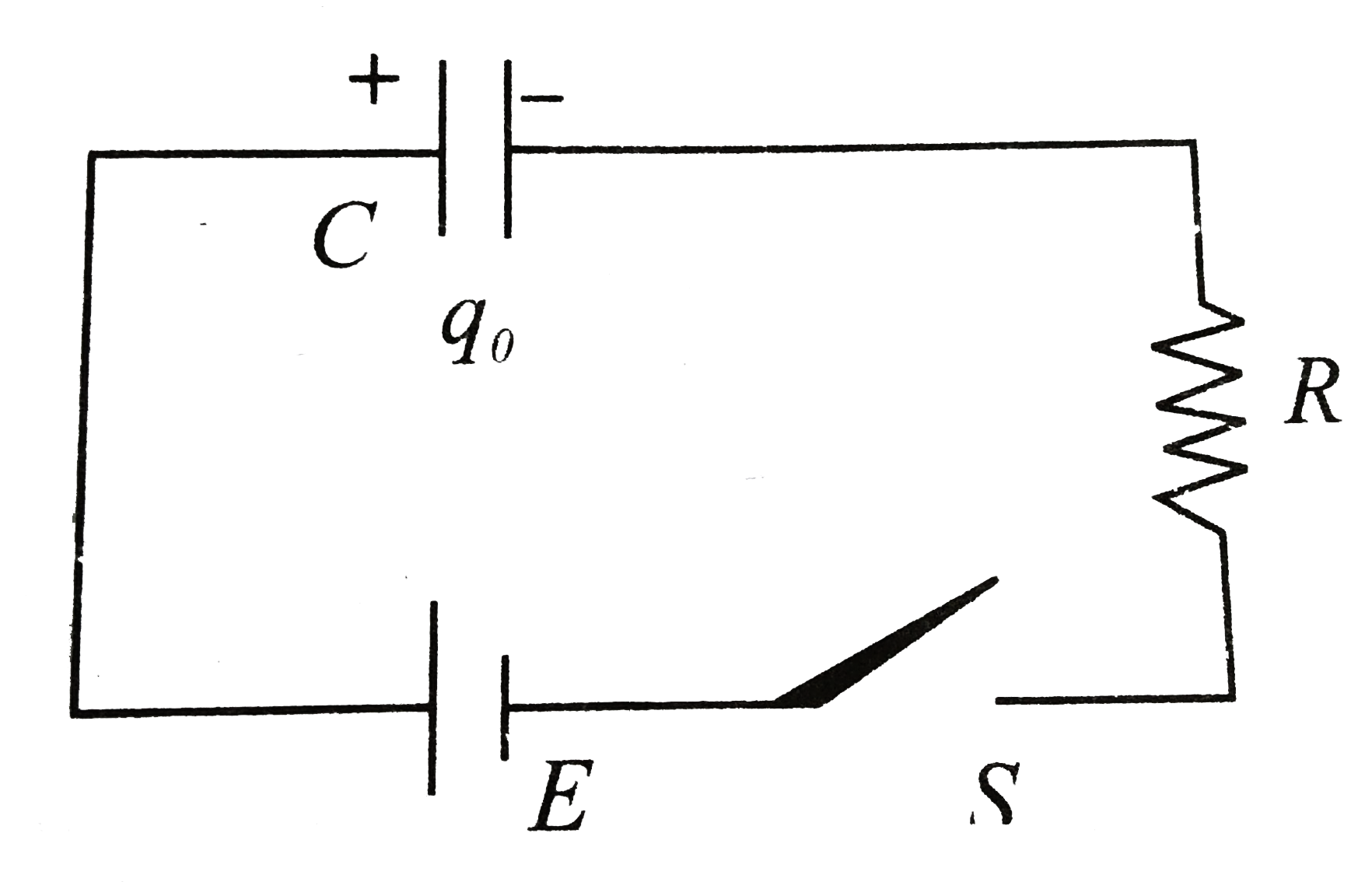
View SolutionA capacitor having initial charge q0=CE/2 is connected to a cell of emf E through a resistor R as shown. Find the total heat generated in the circuit after the switch S is closed.
View SolutionA capacitor C is connected to the two equal resistances as shown in fig. What is the ratio of the time constant during charging and discharging of the capacitance?
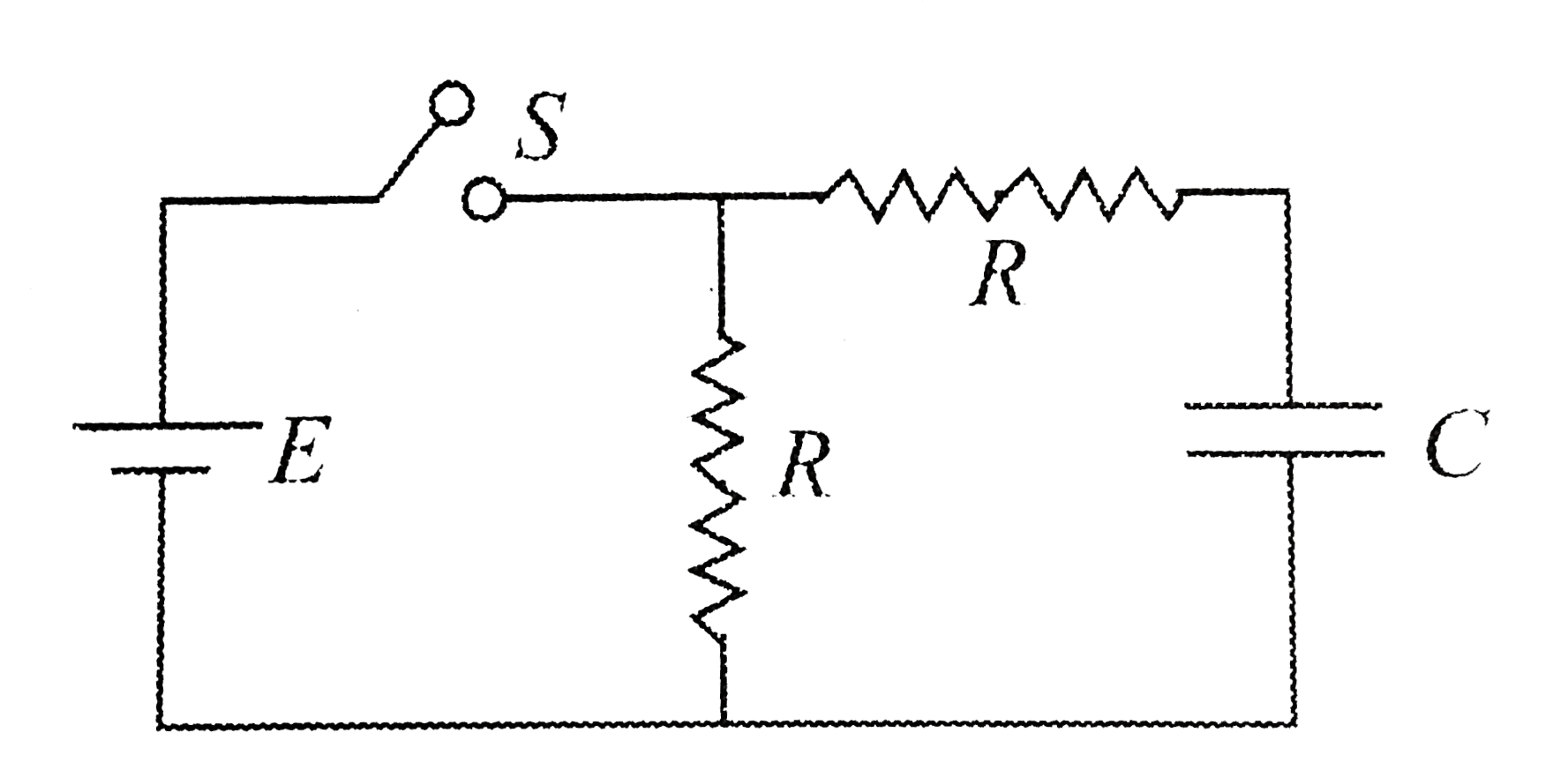
View Solution
