Consider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
The graph of the radial component of E as function of r will be
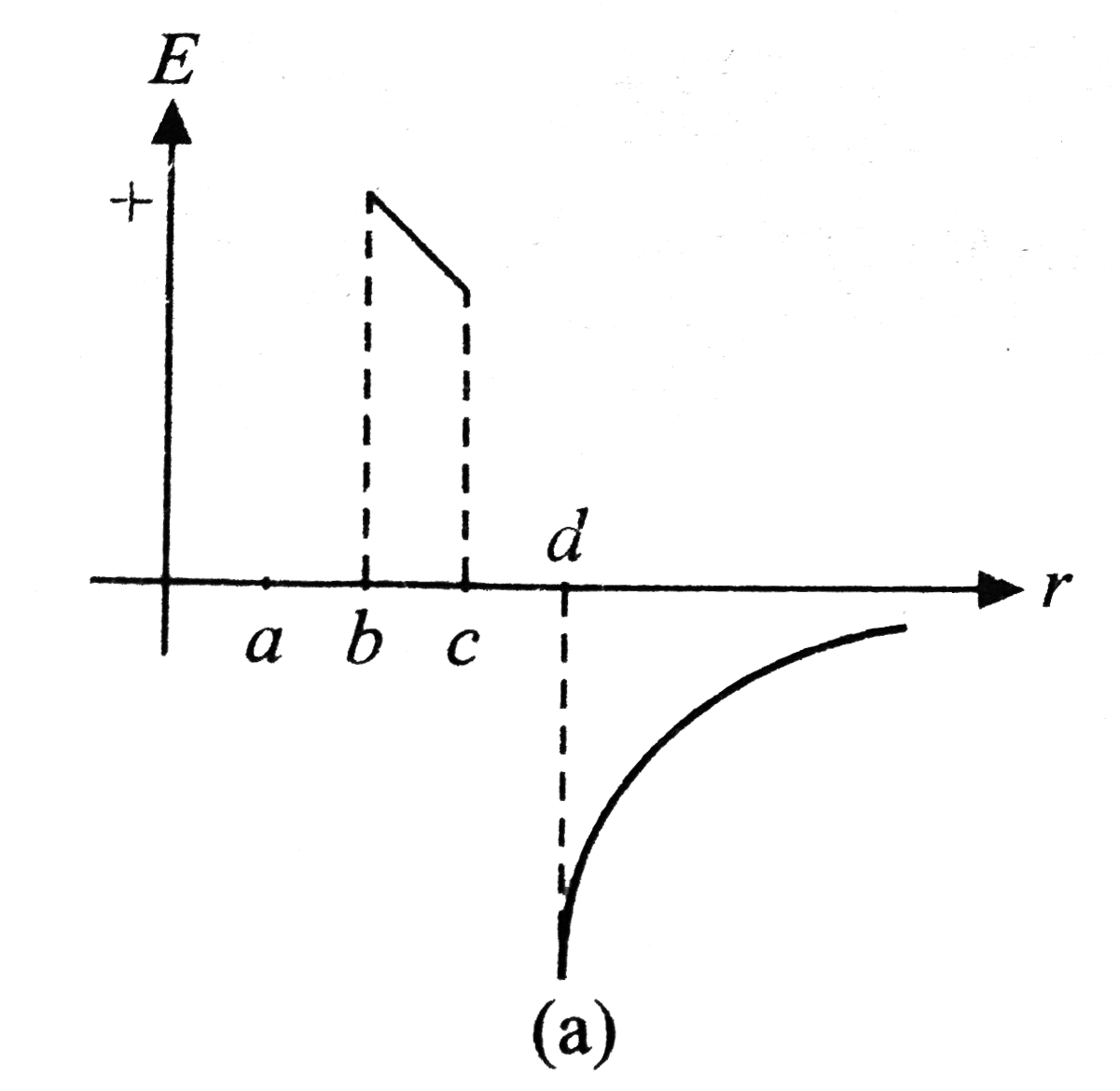

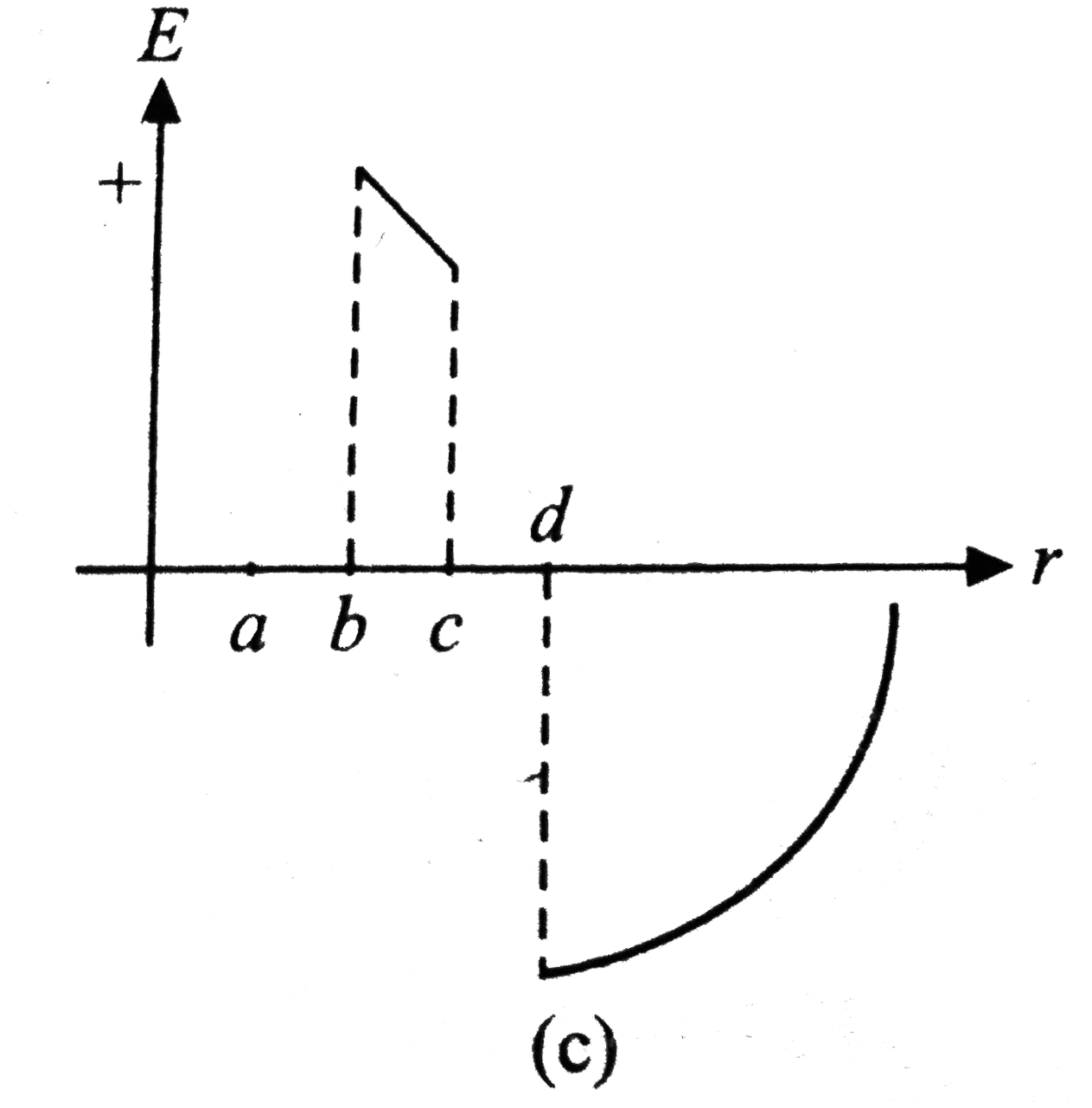

The correct Answer is:B
To solve the problem, we need to calculate the electric field E at different regions defined by the distances r from the common center of the two shells. We have two spherical shells: an inner shell with charge +2q and an outer shell with charge −4q.
1. Identify the Regions:
We will analyze the electric field in three distinct regions:
- Region I: Inside the inner shell ( r<R1 )
- Region II: Between the inner and outer shells ( R1<r<R2 )
- Region III: Outside the outer shell ( r>R2 )
2. Region I: Inside the Inner Shell ( r<R1 ):
- By Gauss's law, the electric field inside a conductor or a shell with no enclosed charge is zero.
- Therefore, E=0 for r<R1.
3. Region II: Between the Shells ( R1<r<R2 ):
- Here, we only consider the charge of the inner shell, since the outer shell's charge does not affect the electric field in this region.
- The enclosed charge Qenc=+2q.
- Applying Gauss's law:
∮→E⋅d→A=Qencϵ0
The area A=4πr2, thus:
E⋅4πr2=2qϵ0
Hence,
E=2q4πϵ0r2=q2πϵ0r2
4. Region III: Outside the Outer Shell ( r>R2 ):
- In this region, we consider the total enclosed charge, which is the sum of the charges of both shells.
- The total enclosed charge Qenc=+2q−4q=−2q.
- Again applying Gauss's law:
E⋅4πr2=−2qϵ0
Therefore,
E=−2q4πϵ0r2=−q2πϵ0r2
Summary of Electric Field in Different Regions:
- For r<R1: E=0
- For R1<r<R2: E=q2πϵ0r2
- For r>R2: E=−q2πϵ0r2
We will analyze the electric field in three distinct regions:
- Region I: Inside the inner shell ( r<R1 )
- Region II: Between the inner and outer shells ( R1<r<R2 )
- Region III: Outside the outer shell ( r>R2 )
- By Gauss's law, the electric field inside a conductor or a shell with no enclosed charge is zero.
- Therefore, E=0 for r<R1.
- Here, we only consider the charge of the inner shell, since the outer shell's charge does not affect the electric field in this region.
- The enclosed charge Qenc=+2q.
- Applying Gauss's law:
∮→E⋅d→A=Qencϵ0
The area A=4πr2, thus:
E⋅4πr2=2qϵ0
Hence,
E=2q4πϵ0r2=q2πϵ0r2
- In this region, we consider the total enclosed charge, which is the sum of the charges of both shells.
- The total enclosed charge Qenc=+2q−4q=−2q.
- Again applying Gauss's law:
E⋅4πr2=−2qϵ0
Therefore,
E=−2q4πϵ0r2=−q2πϵ0r2
- For r<R1: E=0
- For R1<r<R2: E=q2πϵ0r2
- For r>R2: E=−q2πϵ0r2
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
A suface has the area vector →A(2ˆi+3ˆj) what is the flux erof a uniform electric though the area if the field is a→E=4ˆiN/cand→E=4ˆkN/C ?
View SolutionElectric flux through a surface are 10m2 lying in the xy plane is (if→E=ˆi+√2ˆj+√3ˆkN/C)
View SolutionA 10 C charge is given to a conducting spherical shell, and a-3 C point charge is placed inside the shell. For this arrangement, find the correct statement(s).
View SolutionNine wires each of resistance R are connected to make a prism as shown in figure. Find the equivalent resistance of the arrangement across AB
View SolutionIn the figure shown a conducting sphere of inner radius 'a' and outer radius 'b' is given a charge Q. A point charge 'q' is placed in the cavity of this sphere at distance 'x'(<a) away from the centre. Find the electric field intensity and electric potentials at point P (outside the sphere) at distance r>b. Also find the electric potential at point C

View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r<a
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for a lt r lt b
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

b<r<c
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for c lt r ltd
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for The graph of the radial component of E as a function of r will be
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
r<a
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
a<r<b
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
b<r<c
View SolutionConsider the previous problem , let the outer shell have the charge - 4 q . As in the above problem , the inner shell has the charge + 2q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for The graph of the radial component of E as function of r will be
View SolutionConsider the previous problem , let the outer shell have the charge - 4 q . As in the above problem , the inner shell has the charge + 2q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for c lt r lt d
View SolutionConsider the previous problem , let the outer shell have the charge - 4 q . As in the above problem , the inner shell has the charge + 2q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for
View Solution

