Consider two points P1(2,7) and P2(6,15). Write the equation and draw a straight line through these points.
y=2x+3
y=2x+5
y=x+3
2y=2x+3
The correct Answer is:A
Step 1. Obtain the gradient or slope, which is m.
Step 2. c can be found by using the (x,y) values at any given point.
Step 1. Gradient =x2−y1x2−x1=15−76−2=HeightDistance=84=2
So, y=2x+c.
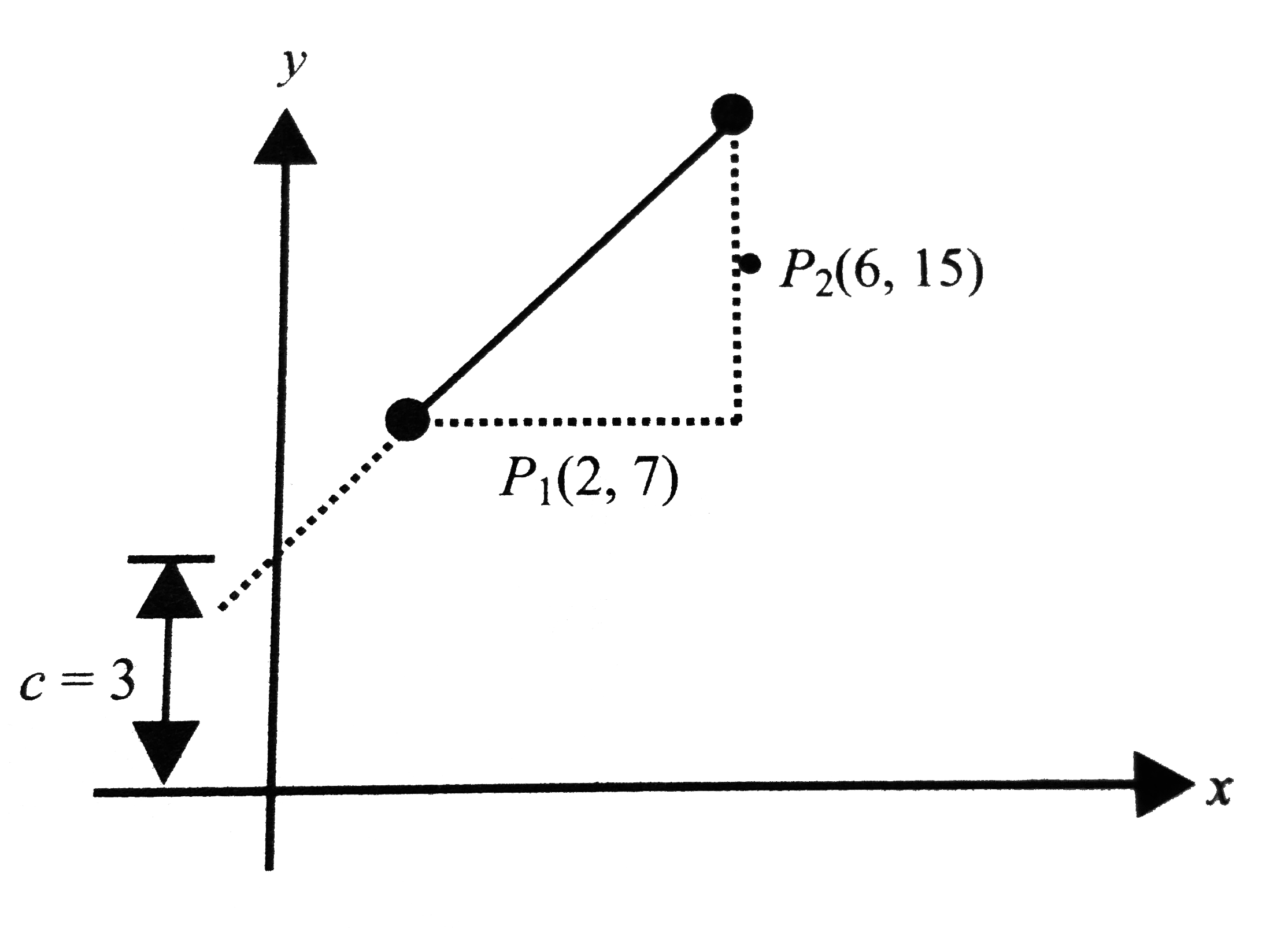
Step 2. To find c, put x=2,y=7 or x=6,y=15 in Eq. (i).
7=2×2+c⇒c=3
So, m=2,c=3.
Hence, the equation becomes y=2x+3.
Topper's Solved these Questions
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Solved Examples
8 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.1
2 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
Similar Questions
From point A located on a highway (figure) one has to get by car as soon as possible to point B located in the field at a distance l from the highway. It is known that the car moves in the field η times slower than on the highway. At what distance from point D one must turn off the highway?

View SolutionExpand (1+x)−2.
View SolutionA 20cm long string, having a mass of 1.0g, is fixed at both the ends. The tension in the string is 0.5N. The string is into vibrations using an external vibrator of frequency 100Hz. Find the separation (in cm) between the successive nodes on the string.
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionWrite the equation of the line through the points (1,1)and (3,5).
View SolutionFind the equation to the line through the point (−4,−3) and perpendicular to the line joining the points (1,3)and2,7).
View SolutionConsider two points P1(2,7) and P2(6,15). Write the equation and draw a straight line through these points.
View Solutionबिंदु (3,5) से होकर एक सरल रेखा इस प्रकार खींची गई है कि इसका दोनों अक्षों के बीच अंतःखंडित भाग इस बिंदु पर समद्विभाजित हो जाता है, तो इस सरल रेखा का समीकरण निकालें।
View SolutionIf P1 and P2 are the lenghts of the perpendicular from the points (2,3,4) and (1,1,4) respectively from the plane 3x-6y+2z+11=0, then P1 and P2 are the roots of the equation
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (-4,3) से होकर जाती है तथा दोनों अक्षों के बीच अन्तः खण्ड खण्डित इस बिन्दु भाग इस बिन्दु पर समद्विभाजित होता है।
View Solutionएक सरल रेखा बिन्दु (−4,−3) से होकर जाती तथा बिन्दुओं (1,3) और (2,7) को मिलाने वाली रेखा पर लम्ब है। इस रेखा का समीकरण ज्ञात कीजिए ।
View SolutionTwo straight lines intersect at a point O. Points P1,P2,...........,Pn on the other . Ithe point O is not to be used, the number of triangles that can be drawn using these points as vertices is :
View SolutionThe equation of the line joining the points (-3,4,11) and (1,-2,7) is
View Solution(4,3) বিন্দুগামী কোনো সরলরেখার অক্ষ দুটির অপর ছেদিতাংশদ্বইয়ের সমষ্টি (−1) হলে সরলরেখার সমিকরণ হবে
View SolutionWrite the equations of the two lines passing through the point (3,10). How many more lines can pass through this point.
View SolutionIf p1,p2 are the perpendicular distance from the origin to the two perpendicular to each other, then the locus of the point of intersection of the perpendicular lines is
View Solution

