Derive an expression for the torque experienced by a dipole due to a uniform electric field .
Torque experienced by an electric dipole in the uniform electric field : Consider an electric dipole of dipole moment →p placed in a uniform electric field →E whose field lines are equally spaced and point in the same direction . The charge +q will experience a force q →E in the direction of the field and charge -q will experience a force -q →E in a direction opposite to the field . Since the external field →E is unform the total force acting on the dipole is zero . These two forces acting at different points will constitute a couple and the dipole experience a torque . This torque tends to rotate the dipole . (Note that electric field lines of a uniform field are equally spaced and point in the same direction). The total torque on the dipole about the point O
→τ=−−→OA×(−q→E)+−−→OB×q→E
Using right -hand corkscrew rule it is found that total torque is perpendicular to the plane of the paper and is directed into it. The magnitude of the total torque τ=∣∣∣−−→OA∣∣∣(−q→E)sinθ+∣∣∣−−→OB∣∣∣∣∣q→E∣∣sinθ
→τ=qE2asinθ
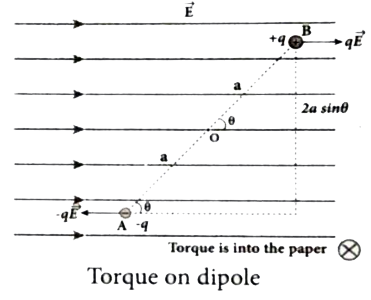
where θ is the angle made by →p with →E . Since p =2aq the torque is written in terms of the vector product as →τ=→p×→E
The magnitude of this torque is τ=pE sin θ and is maximum when θ=90∘
This torque tends to rotate the dipole and align it with the electric field→E . Once →p is aligned with →E the total torque on the dipole becomes zero.
Similar Questions
a) Define an ideal electric dipole. Give an example.
b) Derive an expression for the torque experienced by an electric dipole in a uniform electric field. What is net force acting on this dipole.
c) An electric dipole of length 2cm is placed with its axis making an angle of 60∘ with respect to uniform electric field of 105N/C. If it experiences a torque of 8√3 Nm, calculate the (i) magnitude of charge on the dipole, and its potential energy
View SolutionDerive an expression for the torque acting on an electric dipole placed in a uniform electric field.
View SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torque →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is:
(i) maximum (ii) zero
View SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torquet →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is :
zero
View SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torquet →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is :
maximum
View SolutionFind the expression of torque acting on an electric dipole placed in a uniform electric field . Using the above obtained expression of torque find the expression for potential energy of electric dipole kept in the uniform electric field . Assume potential energy of electric dipole to be zero when its axis is perpendicular to the externally applied electric field .
View SolutionDerive an expression for torque →τ experienced by an electric dipole of dipole moment →p kept in uniform electric →E. What will happen if the field were not uniform?
View SolutionObtain the expression for the torque →τ experienced by an electric dipole of dipole moment →p in a uniform electric field, →E. What will happen if the field were not uniform?
View SolutionDerive the expression for the torque acting on an electric dipole, when it is held in a uniform electric field. Identify the orientation of the dipole in the electric field, in which it attains stable equilibrium.
View SolutionWhen is the torque acting on an electric dipole placed in a uniform electric field maximum?
View Solution

