Derive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.Solution in Tamil
Consider a uniform ring of mass M and radius R . Let us find the moment of inertia of thering about an axis passing through its centre and perpendicular to the plane. Let us take an infinitesimally small mass (dm) of length (dx) of the ring. This (dm) is located at a distance R, that is the radius of the ring from the axis as shown in figure.
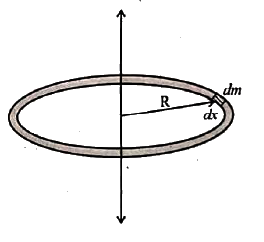
The moment of inertia (dI) of this small mass (dm) is
dI=(dm)R2
The length of the ring is its circumference (2R). As the mass is uniformly distributed, the mass per unit length (λ) is
λ=masslength=M2πr
The mass (dm) of the infinitesimally small length is dm =λdx=M2πrdx
Now the moment of inertia (I) of the entire ring is
I=∫dI=∫(dm)R2
=∫(M2πRdx)R2
I=MR2π∫dx
In order to cover the entire length of the ring, the limits of integration are taken from 0 to 2πR.
I=MR2π∫2πr0dx
I=MR2π[x]2πR0=MR2π[2πR−0]
I=MR2
Similar Questions
Calculate the moment of inertia of a ring about an axis passing through centre of the ring and perpendicular to the plane of the ring.
View SolutionDerive the expression for moment of inertia of a uniform ring about an axis passing thorugh the centre and perpendicular to the plane.
View SolutionDerive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I . Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionState an expression for moment inertia of a thin uniform disc about an axis passing through its centre and perpendicular to its plane .
View Solution
