Explain how, friction enables us to walk without slipping.
Step-by-Step Solution:
1. Understanding Friction: Friction is a force that opposes the relative motion between two surfaces in contact. In the context of walking, it occurs between the soles of our shoes and the ground.
2. Role of Friction in Walking: When we walk, friction prevents us from slipping. It provides the necessary grip between our feet and the ground, allowing us to maintain balance and control.
3. Movement Mechanics: To walk, we lift one foot off the ground while pushing the other foot backward. This action creates a backward force on the ground.
4. Frictional Force Direction: As we push the ground backward with one foot, the frictional force acts in the opposite direction (forward) on that foot. This frictional force propels us forward, allowing us to take a step.
5. Continuous Process: This process is continuous; as one foot pushes backward and the other foot lifts, the frictional force keeps acting, enabling us to walk without slipping.
Summary:
Friction between our shoes and the ground is essential for walking. It allows us to push against the ground without slipping, enabling forward movement and balance.
---
Friction between our shoes and the ground is essential for walking. It allows us to push against the ground without slipping, enabling forward movement and balance.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination θ ?
A27tanθB13tanθC12tanθD25tanθA sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
A2/5tanθB2/7tanθC5/7tanθDtanθA spherical shell of radius R is rolling down an incline of inclination θ without slipping. Find minimum value of coefficient of friction.
 A27tanθB25tanθC23tanθDNone
A27tanθB25tanθC23tanθDNone
Explain the process which enables us to perceive motion in a cartoon film.
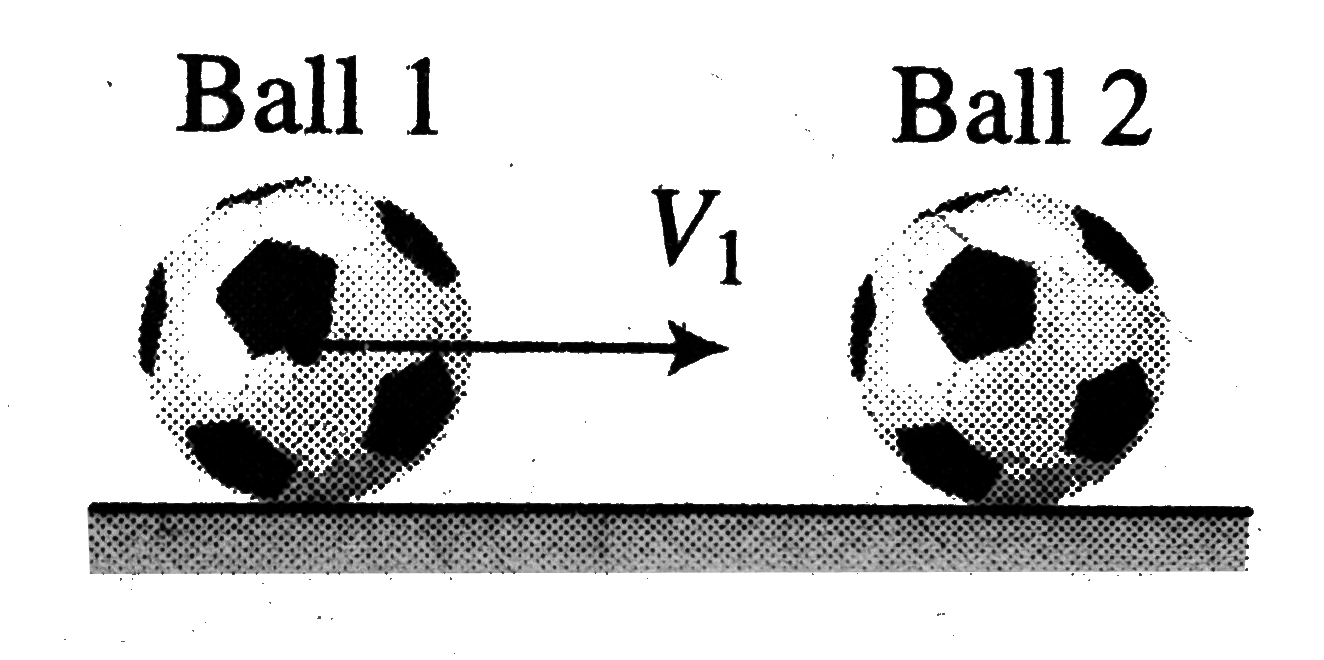
View SolutionA solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.
View SolutionThe ratio of the accelerations for a solid sphere (mass m,andradiusR) rolling down an incline of angle θ without slipping, and slipping down the incline without rolling is
View SolutionThe ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is
View SolutionA solid sphere is thrown up a rough incline. The sphere rolls up without slipping and eventually comes down rolling without slipping. The direction of friction during upward and downward motion respectively is :-
View Solution