Explain how the image is formed by thin convex lens and derive −1u+1v=(n21−1)[1R1+1R2]Solution in Gujrati
Figure shows the geometry of image formation by a double convex lens. The image formation can be seen in terms of two steps.
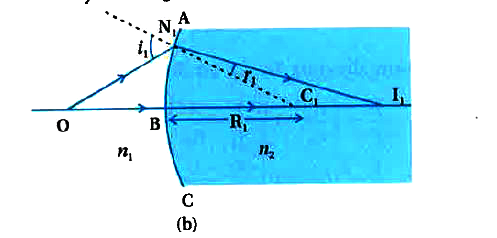
The first refracting surface forms the image I1, of the object O figure (b).
The image I1, acts as a virtual object for the second surface that forms the image at I figure (c).

Thus, the image formed by thin lens is shown in figure (a).

For refraction at interface ABC,
∴n1OB+n2BI1=n2−n1BC1 ... (1)
A similar procedure applied to the interface ADC gives,
∴−n2DI1+n2DI=n2−n1DC1 ... (2) (Refractive index of medium on right side of ADC is n, while on its left it is n2).
For a thin lens, BI1, = DI1. Adding equations (1) and (2),
n1OB+n1DI=(n2−n1)[1BC1+1DC2]
Suppose the object is at infinity i.e. OB →∞ and DI = f.
∴n1∞+n2f=(n2−n1)[1BC1+1DC2]
∴n1f=(n2−n1)[1R1−1R2]
[∵BC1=R1 and DC2=−R2]
Now dividing by n1 on both sides 1∞=0
∴1f=(n2n1−1)[1R1−1R2]
∴1f=(n21−1)[1R1−1R2](∵n21=n2n1) ... (3)
equation (3) is known as the lens maker.s formula.
It is useful to design lenses of desired focal length using surfaces of suitable radii of curvature.
Note that the formula is true for a concave lens also. In that case R, is negative, R, positive and therefore f is negative.
Similar Questions
Derive lens formula [1v−1u=1f] for a thin convex lens, using diagram for the formation of a real image by convex Lens.
View SolutionDerive Lens formula for [frac(1)(v)-frac(1)(u)= frac(1)(f)] a thin convex Lens, using ray diagram for the formation of a real image by Convex Lens.
View Solution(1r1+1r2)(1r2+1r3)(1r3+1r1) =
View SolutionNature of the graph between 1//u and 1//v for a convex lens, where u is the distance of the object and v is that of image is
View SolutionDerive the lens formula 1/f=1/v-1/u for a convex lens.
View SolutionFor a convex lens for any image prove that 1v−1u=1f.
View SolutionUse the lens equation 1v+1u=1f and prove that for a convex lens when the object is placed within the focal length, the image will be virtual.
View SolutionLet f(x)=sinxandg(x)=(log)e|x| If the ranges of the composition functions fogandgof are R1andR2, respectively then (a) R1{u:−1≤u<1},R2={v:−∞v<0} (b) R1={u:−∞<u<0},R2={v:−∞<v<0} (c) R1={u:−1<u<1},R1={v:−∞V≤0}
View Solution
