
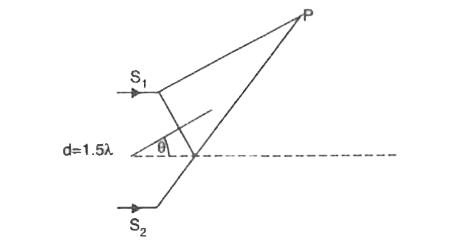
Fig. Shows two coherent sources S1 and S2, emitting wavelength λ.The separation S1S2=1.51.S1 is ahead in phase by π2 relative to S2.The maxima occurs in a direction given by sin−1 of :
0
12 only
16 only
12−16and−56
The correct Answer is:D
δ is phase difference of waves between S1 and S2 at pt. P
δ=(2πλdsinθ+π2)
For maxima at P,
δ=nπ,n=0,±1,±2...
∴2πλ.dsinθ+π2=nπ
2πλ(1.5λsinθ)=(n−12)π
∴3sinθ=(n−12)
∴sinθ=(n−12)3
For n = 0 "sinθ=−16
n=±1sinθ=16,−12
n=±2sinθ=12,−56
Similar Questions
Let S1,S2,......S101 be consecutive terms of A.P. If 1S1S2+1S2S3+......+1S100S101=16 and S1+S101=50, then |S1−S101| is equal to
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance >. Each source emits light of wavelength λ where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Which of the following is correct ?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs ?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs ?
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda . The separation between the sources is 2lambda . Consider a line passing through S_(2) and perpendicular to line S_(1) S_(2) . Find the position of farthest and nearest minima. .
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
View SolutionFigure shows two coherent sources S1 and S2 emitting wavelength λ. The separation S1S2=1.5λ and S1 is ahead in phase by π/2 relative to S2 Then the maxima occur in direction θ given by sin−1 of
(i) 0 (ii) 1/2 (iii) −1/6 (iv) −5/6
Correct option are

View Solution

