Find an experssion for the acceleration of the particle and hence indicate its direction .
Acceleration of the particle,
→a=d→vdt=rω(−cosθˆi−sinθˆj)dθdt
=−rω2(cosθˆi+sinθˆj) [∵ω=constant]
= −ω2→r
∴→aand→r are acted in opposite direction.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:CHHAYA PUBLICATIONChapter:CIRCULAR MOTIONExercise:EXAMINATION ARCHIVE WITH SOLUTIONS (WBJEE)
Explore 2 Videos
- CIRCULAR MOTIONBook:CHHAYA PUBLICATIONChapter:CIRCULAR MOTIONExercise:EXAMINATION ARCHIVE WITH SOLUTIONS (JEE MAIN)
Explore 1 Video
- CIRCULAR MOTIONBook:CHHAYA PUBLICATIONChapter:CIRCULAR MOTIONExercise:INTEGER ANSWER TYPE
Explore 3 Videos
- CALORIMETRYBook:CHHAYA PUBLICATIONChapter:CALORIMETRYExercise:EXAMINATION ARCHIVE
Explore 5 Videos
- DOPPLER EFFECT IN SOUND Book:CHHAYA PUBLICATIONChapter:DOPPLER EFFECT IN SOUND Exercise:CBSE SCANNER
Explore 2 Videos
Similar Questions
A particle starts from rest (at x=0) when an acceleration is applied to it. The acceleration of the particle changes with its co-ordinate as shown in the fig. Find the speed of the particle at x=10m.
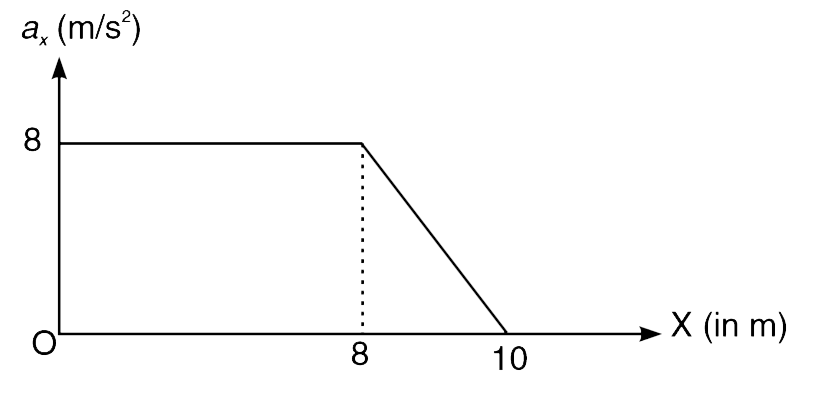
View SolutionIf the acceleration of a particle remains constant in magnitude but not in direction, is its path necessarily a straight line or a circle ?
View Solution
Knowledge Check
For any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
vaca=10ˆi+15ˆj+20ˆk
Find the tangential acceleration of the particle at the given instant :-A17(4ˆi+3ˆj)B175(4ˆi+3ˆj)C17(4ˆi−3ˆj)D175(4ˆi−3ˆj)
Give examples for the particle where (a) the velocity is in opposite direction to the acceleration (b)the velocity of the particle is zero but is acceleration is not zero.
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the tangential acceleration of the particle at the given instant :-
View SolutionFigure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
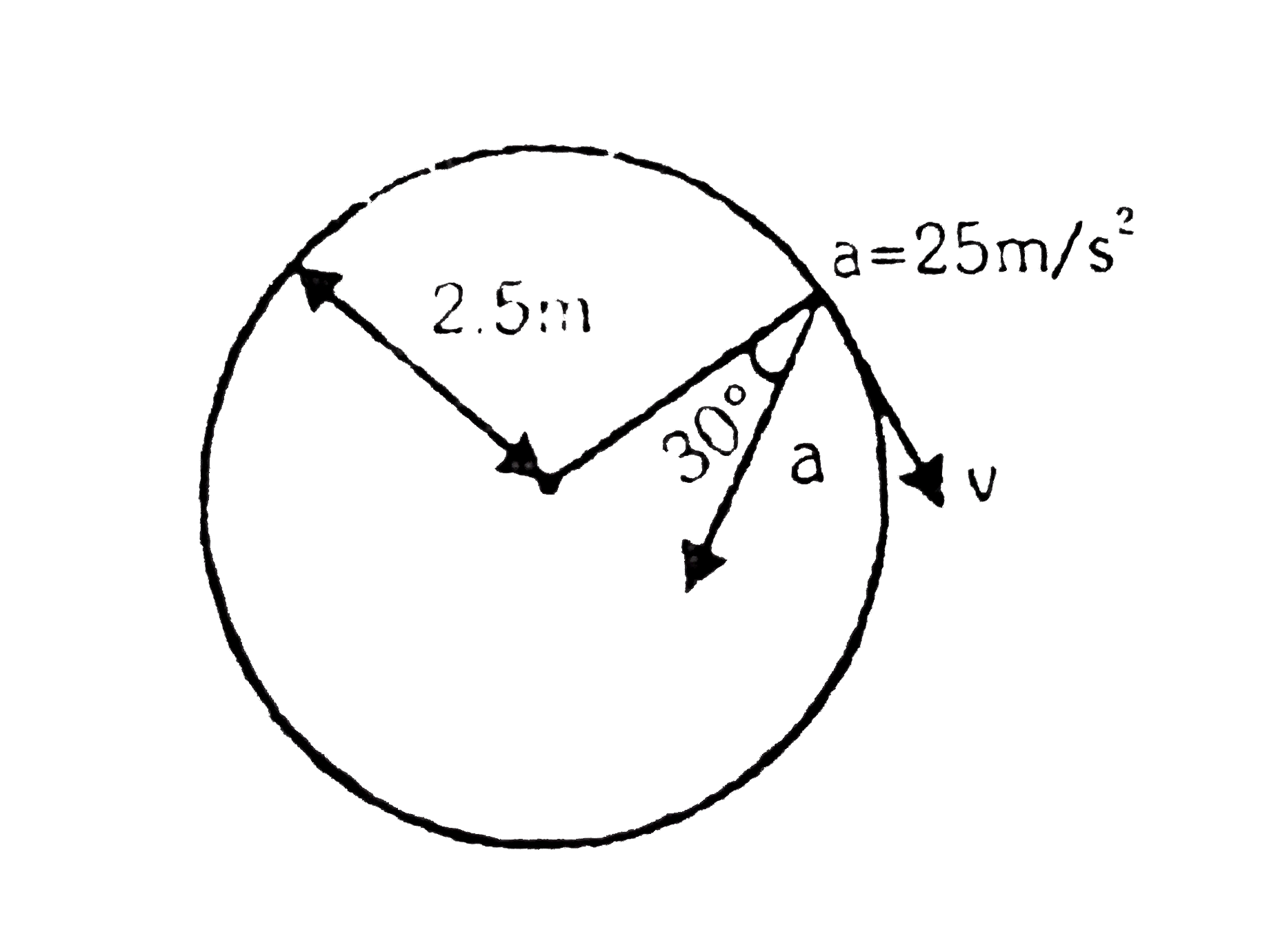
View SolutionA particle is projected from the origin in X-Y plane. Acceleration of particle in Y direction is a. If equation of path of the particle is y=ax−bx2, then find initial velocity of the particle.
View SolutionWrite the direction ratios of the vector r=ˆi−ˆj+2ˆk and hence calculate its direction cosines.
View SolutionWrite the direction ratios of the vector r=ˆi−ˆj+2ˆk and hence calculate its direction cosines.
View SolutionGive examples where a. the velocity of a particle is zero but its acceleration is not zero. b.the velocity is opposite in direction to the acceleration, c. the velocity is perpendicular to the acceleration.
View Solution

