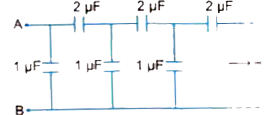
Find the capacitance of the infinite ladder between points X and Y, Fig.
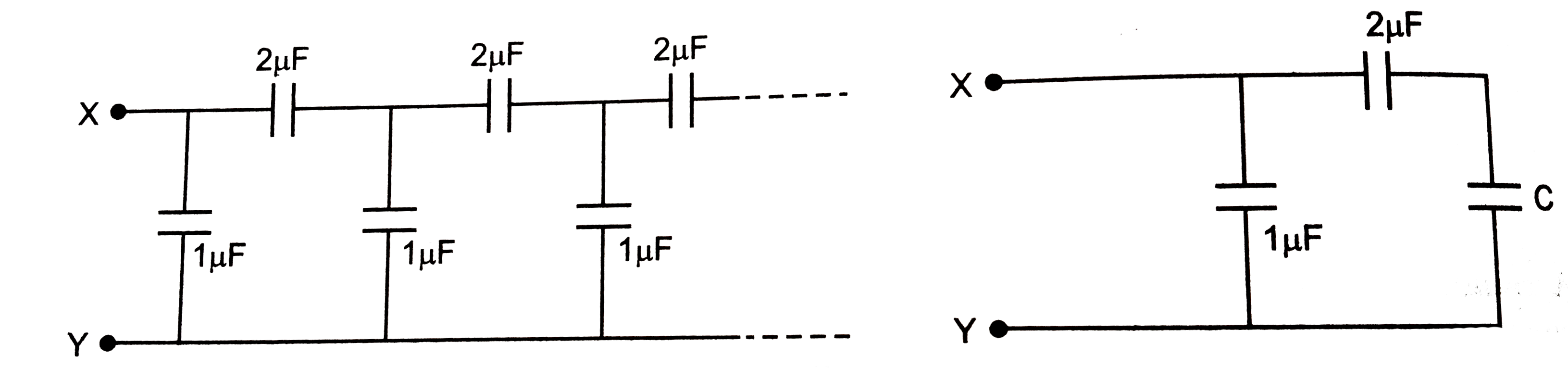
Let C be the capacitance of the infinite ladder. As the ladder is infinite, addition of one more element of two capacitors (1μFand2μF) across the points X and Y should not charge the total capacitance. Therefore, In fig, 2μF capacitance is in series with capacitance C.
∴ Their combined capacity =2×C2+C
This combination is in parallel with 1μF capacitance. The equivalent capacity of the arrangement is
(1+2C2+C) which must be equal to C i.e., (1+n2C1+C)=C
or C2+2C=2+3C or C2−C=0∴C=2or−1
Capacitance cannot be negative. ∴C=2μF
Similar Questions
Knowledge Check
An infinite ladder is constructed by connecting several sections of 2 μF,4μF capacitor combination as shown in figure . It is terminated by a capacitor of capacitance C. What value should be chosen for C such that the equivalent capacitance of the ladder between points A and B becomes independent of the number of sections in between
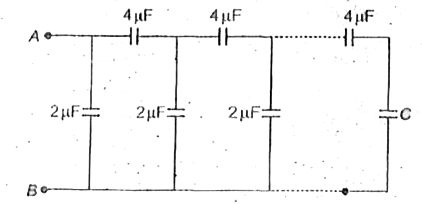 A18μ FB6μ FC2μ FD4μ F
A18μ FB6μ FC2μ FD4μ F
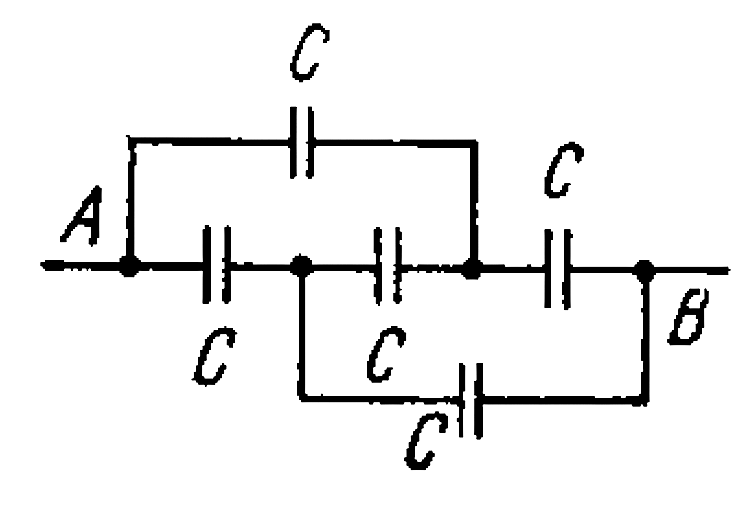
Find the capacitance of the circuit shown in Fig, between points A and B.

View SolutionFind the equivalent capacitance of the circuit between point A and B.
View SolutionFind the equivalent capacitance of the circuit between point A and B.
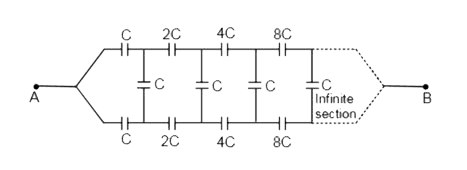
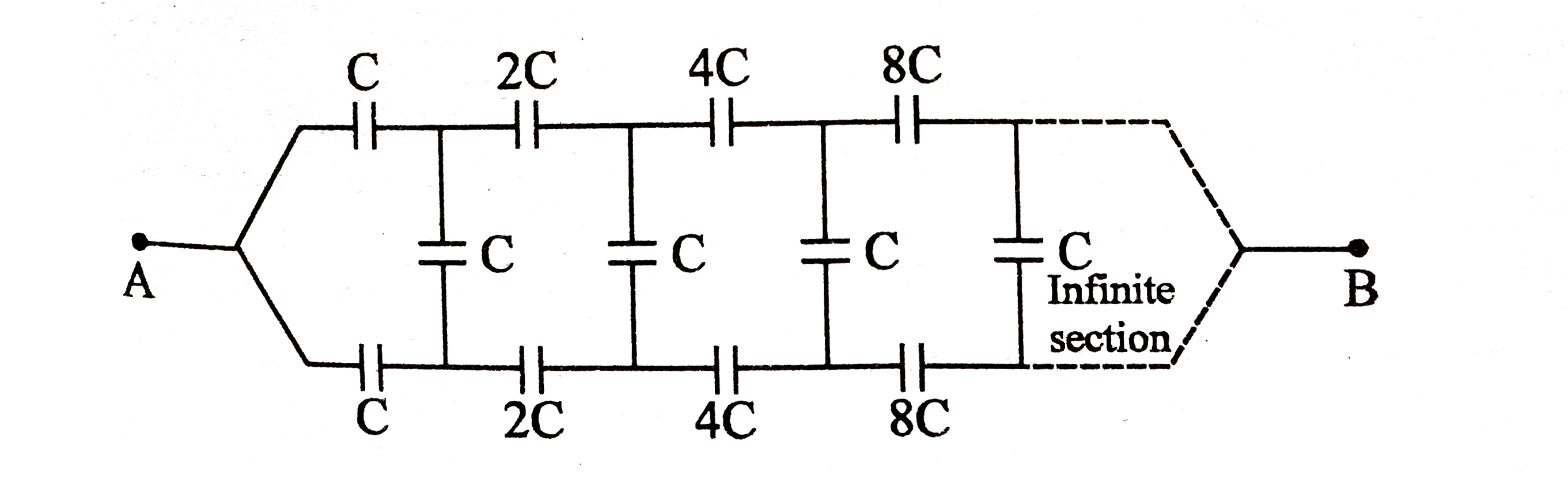
View SolutionFind the equivalont capacitance of the infinite ladder shown in the figure (a) between the points A and B .
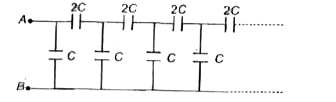
View SolutionFind the equivalent capacitance of the infinite ladder shown in figure between the points A & B.
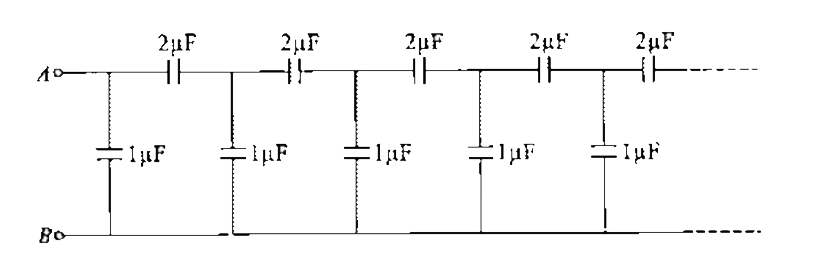
View SolutionFind the capacitance of a system of identical capacitors between points A and B are shown in
(a) Fig. A (b) Fig B
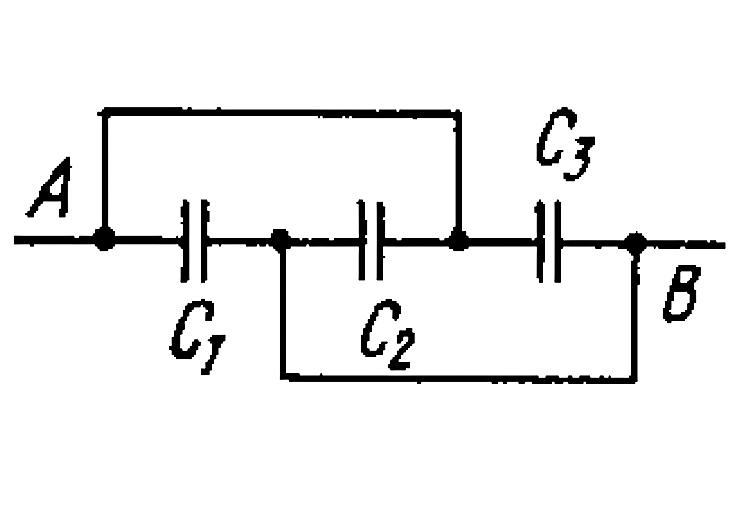
View SolutionA finite ladder circuit is constructed by connecting several sections of 6μF,8μF capacitor combinations as shown in the figure. Circuit is terminated by a capacitor of capacitance C. Find the value of C, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between ?

View Solution