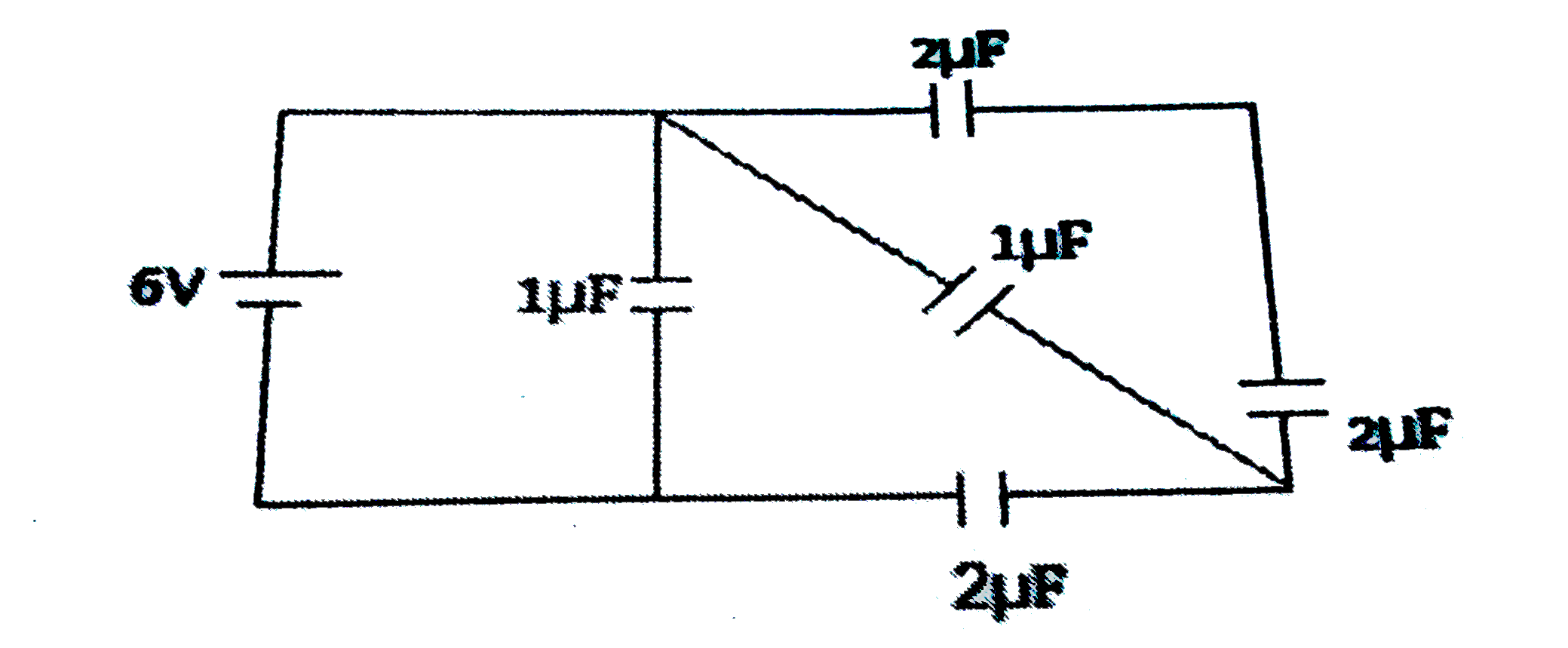
Find the total energy stored in the capacitors in the given network of Fig.
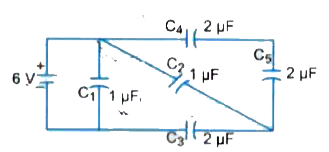
In fig , capacitors C4 and C5 of 2μF each are in series , their equivalent capacitance
C.=C4C5C4+C5=2×22+2=1μF
Now C. and C2 are in parallel , hence their equivalent capacitance
C..=C2+C.=1+1=2μF
Further C.. and C3 are in series , their equivalent capacitance
C0=C..C3C..+C3=2×22+2=1μF
Now C. and C2 are in parallel , hence their equivalent capacitance C..=C2+C.=1+1=2μF
Further C.. and C3 are in series , their equivalent capacitance
C0=C..C3C..+C3=2×22+2=1μF
Finally , C0 is in parallel with C1 , hence net resultant capacitance C=C0+C1=1+1=2μF
∴ Total energy stored in the capacitors in the given network
U=12CV2=12×2×10−6×(6)2=3.6×10−5J
Similar Questions
Knowledge Check
Find out total energy stored in the capacitors.
A500μJB300μJC600μJD1300μJEnergy Stored in the capacitor is
Aε0E2×AdB(12)ε0E2×AdCε0E2×AdDε0E×AdFind the total energy stored in capacitors in the network shown in Fig.
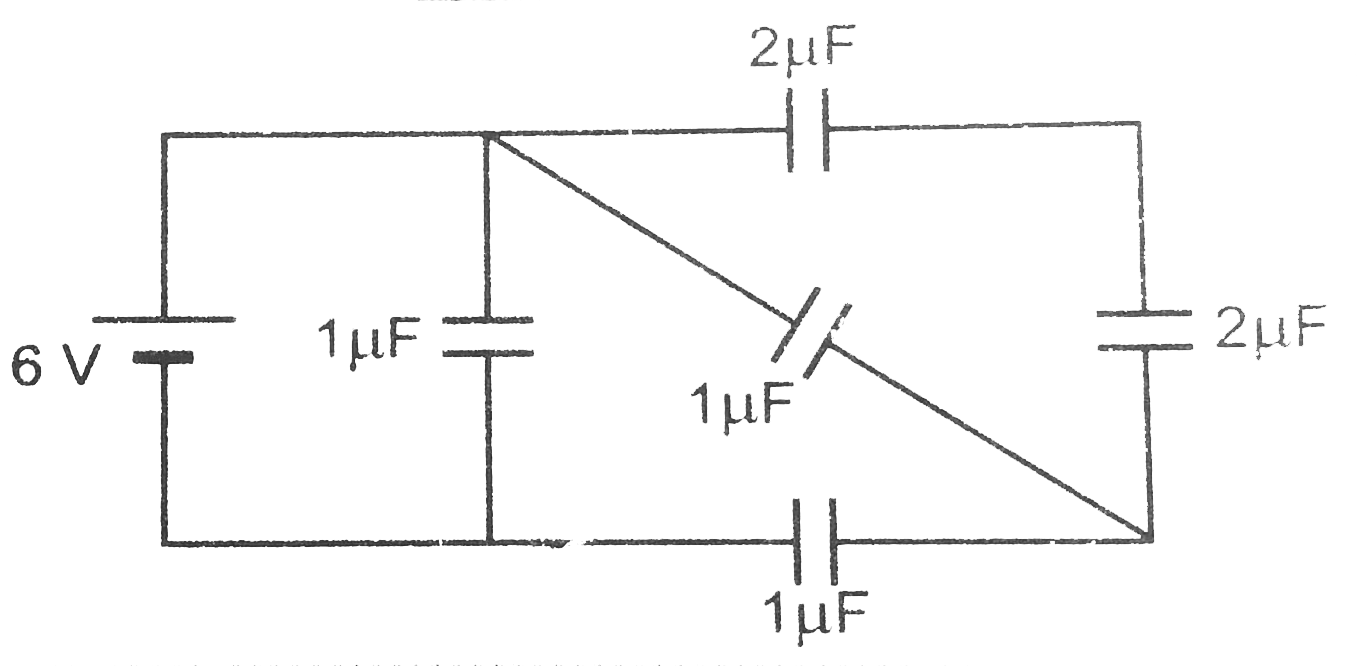 A3.6 × 10 − 5 JB0.6 × 10 − 5 JC5.6 × 10 − 5 JDnone of these
A3.6 × 10 − 5 JB0.6 × 10 − 5 JC5.6 × 10 − 5 JDnone of these
A battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
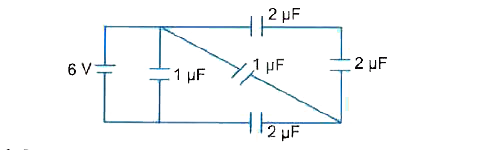
View SolutionFind total energy stored in capacitors given in the circuit.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View Solution