Force acting on a block moving along x-axis is given by
F=−(4x2+2)N
The block is displaced from x=−2m to x=+4m, the work done will be
positive
negative
zero
may be positive or negative
The correct Answer is:B
To find the work done on the block as it moves from x=−2m to x=4m under the influence of the force F=−4x2+2N, we will follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a variable force along a straight path is given by the integral of the force over the displacement:
W=∫x2x1Fdx
where x1 is the initial position and x2 is the final position.
Step 2: Set Up the Integral
In this case, we need to calculate:
W=∫4−2−4x2+2dx
Step 3: Evaluate the Integral
We can simplify the integral:
W=−4∫4−21x2+2dx
The integral ∫1x2+a2dx is known to be 1atan−1(xa)+C. Here, a2=2 implies a=√2.
Thus, we have:
∫1x2+2dx=1√2tan−1(x√2)+C
Step 4: Calculate the Definite Integral
Now we need to evaluate:
W=−4(1√2tan−1(x√2))4−2
Calculating the limits:
1. For x=4:
tan−1(4√2)=tan−1(2√2)
2. For x=−2:
tan−1(−2√2)=tan−1(−√2)
Step 5: Substitute the Limits
Now substituting the limits into the integral:
W=−4(1√2(tan−1(2√2)−tan−1(−√2)))
Step 6: Simplify the Expression
Using the property of the arctangent function:
tan−1(−x)=−tan−1(x)
Thus:
W=−4(1√2(tan−1(2√2)+tan−1(√2)))
Step 7: Final Calculation
Now we can compute the numerical values of tan−1(2√2) and tan−1(√2) using a calculator and substitute them back into the equation to find the work done.
Conclusion
The work done W will be negative since the force is acting opposite to the direction of displacement.
The work done W by a variable force along a straight path is given by the integral of the force over the displacement:
W=∫x2x1Fdx
where x1 is the initial position and x2 is the final position.
In this case, we need to calculate:
W=∫4−2−4x2+2dx
We can simplify the integral:
W=−4∫4−21x2+2dx
The integral ∫1x2+a2dx is known to be 1atan−1(xa)+C. Here, a2=2 implies a=√2.
∫1x2+2dx=1√2tan−1(x√2)+C
Now we need to evaluate:
W=−4(1√2tan−1(x√2))4−2
1. For x=4:
tan−1(4√2)=tan−1(2√2)
tan−1(−2√2)=tan−1(−√2)
Now substituting the limits into the integral:
W=−4(1√2(tan−1(2√2)−tan−1(−√2)))
Using the property of the arctangent function:
tan−1(−x)=−tan−1(x)
Thus:
W=−4(1√2(tan−1(2√2)+tan−1(√2)))
Now we can compute the numerical values of tan−1(2√2) and tan−1(√2) using a calculator and substitute them back into the equation to find the work done.
The work done W will be negative since the force is acting opposite to the direction of displacement.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:A Only One Option is Correct
Explore 42 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
Consider a variable force F=(3x+5)N acting on a body and if it is displaced from x=2m to x=4m, calculate the work done by this force.
View SolutionA force→F=(7−2x+3x2) N is applied on a 2 kg mass which displaces it from x = 0 to x = 5 m. Work done in joule is -
View SolutionA positon dependent force ,F=8−4x+3x2N acts on a small body of mass 2 kg and displaces it from x=0 to x=5 m. The work done in joule is
View SolutionThe velocity of a block of mass 2kg moving along x− axis at any time t is givne by v=20−10t(m/s) where t is in seconds and v is in m/s. At time t=0, the block is moving in positive x− direction.
The Kinetic energy of block at t=3sec. is :
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionA force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
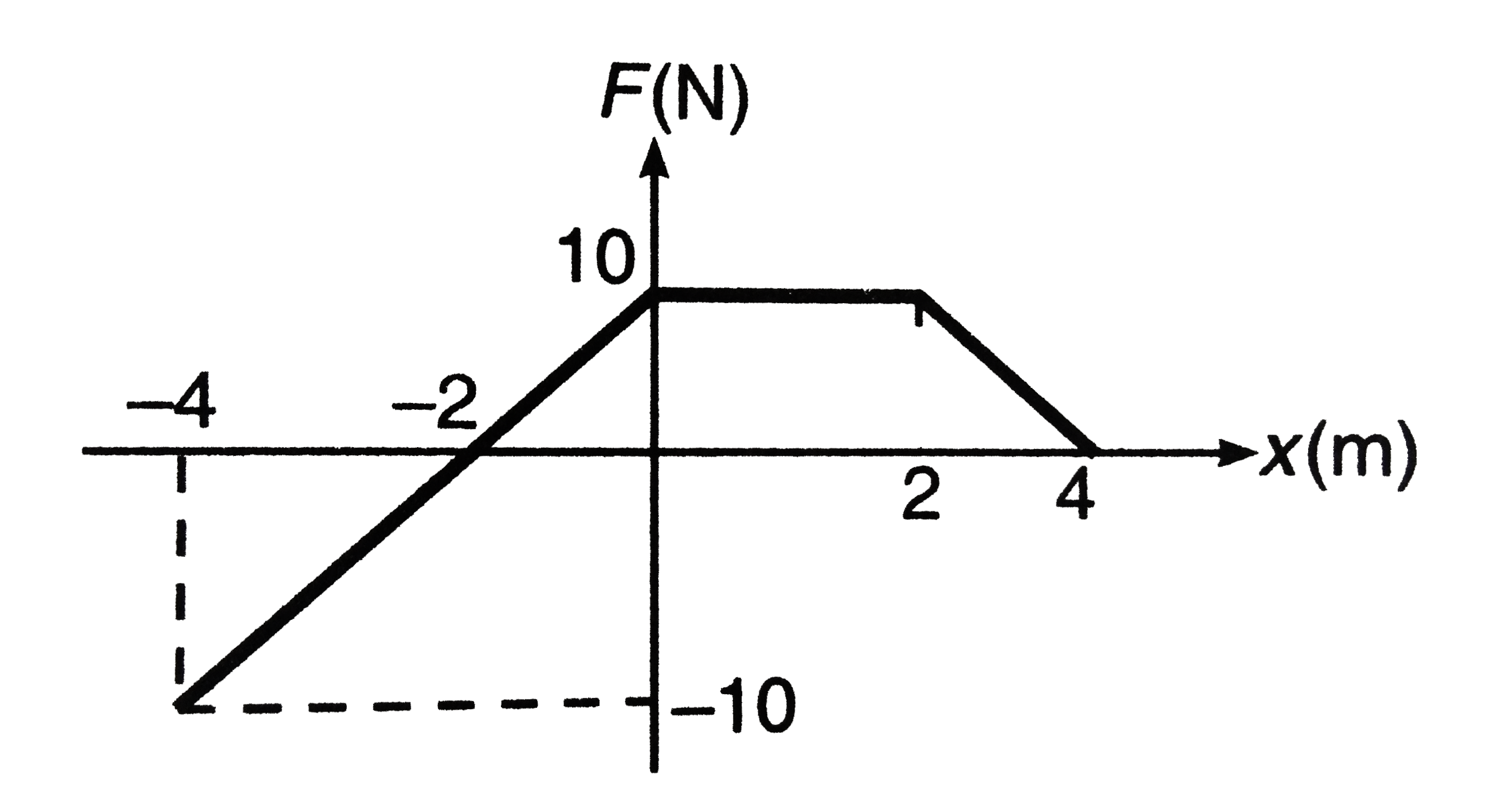 .
.
View SolutionThe work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View SolutionThe relationship between the force F and position x of body is as shown in figure. The work done in displacing the body in displacing the body from (x=1m to x=5m) will be
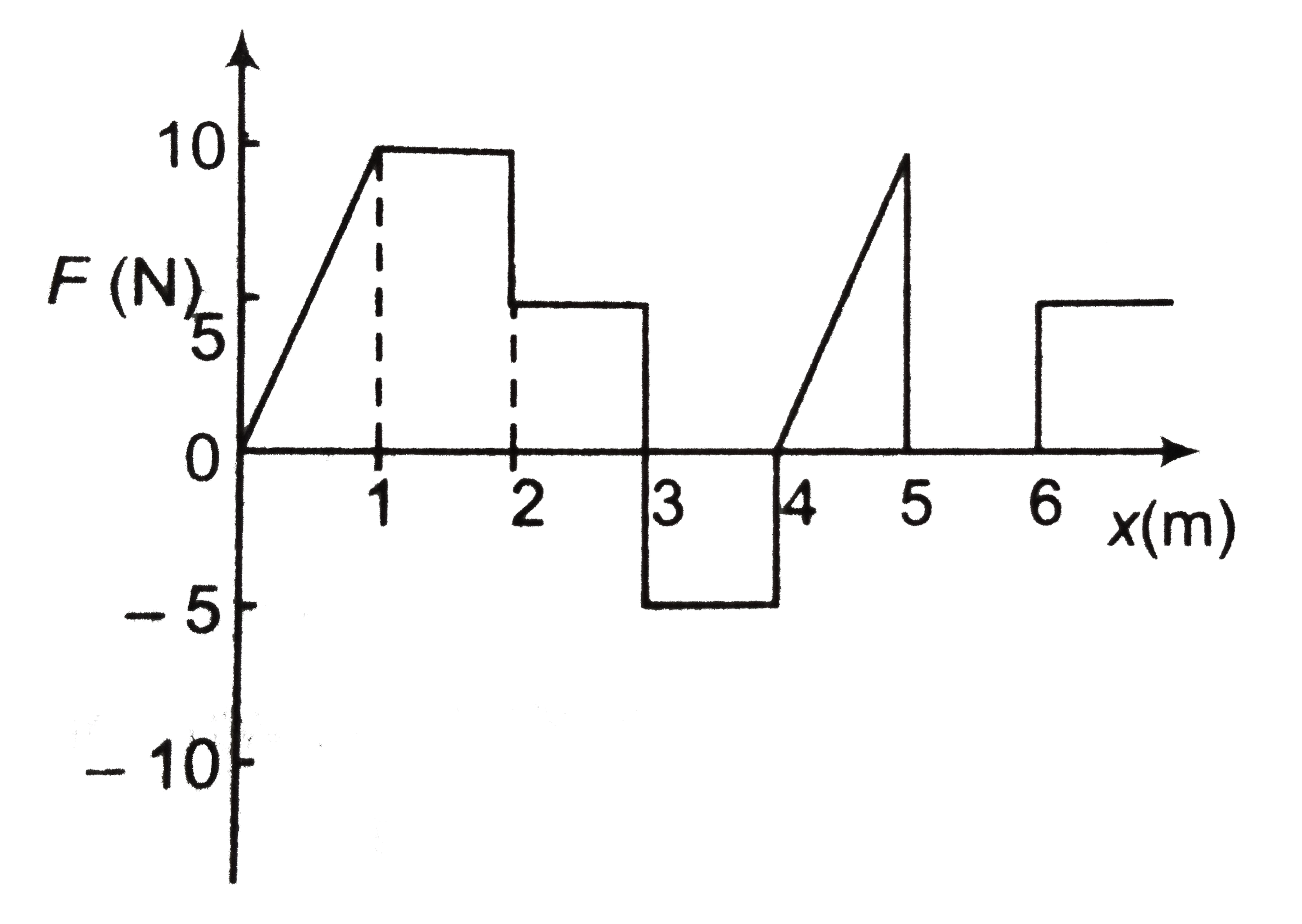 .
.
View Solution
