From a single source, two wave trains are sent in two different string. The two wave equations are ((area of corss-section and tension of both string are same y1 = A sin (w1t−k1x)andy2=2Asin(w1t−k2z)Suppose u = energy density , P = power trasmitted and I = intensity of the wave, then match the following. 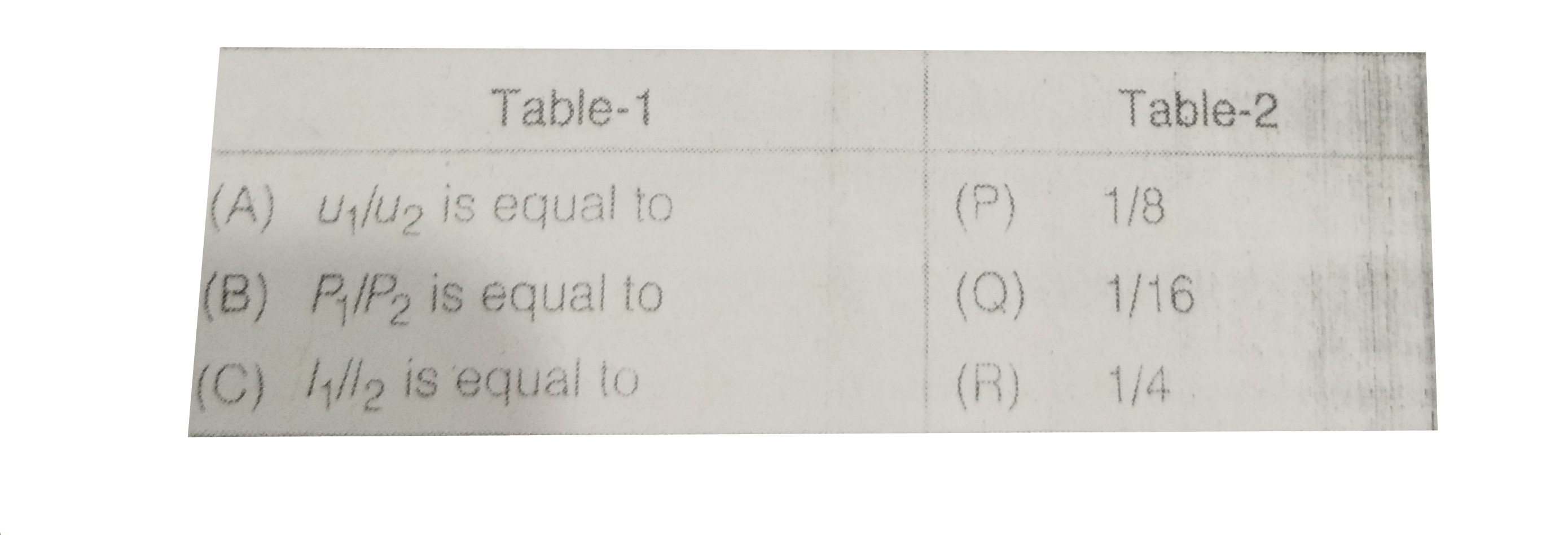
The correct Answer is:(a)Q, (b)P, (c )P
Similar Questions
Statement - 1 : Two longitudinal waves given by equations : y_(1) (x,t) = 2 a sin (omega t- kx) and y_(2) (x,t) = a sin (2 omega t - 2kx) will have equal intensity . Statement -2 : Intensity of waves of given frequency in same medium is proportional to square of amplitude only .
View SolutionThe two waves are displayed as follows y_(1)=a sin omega t y_(2)=a cos omega t The first wave is from the second …………………
View SolutionA standing wave is maintained in a homogeneous string of cross-sectional area s and density rho . It is formed by the superposition of two waves travelling in opposite directions given by the equation y_(1)=a sin(omegat -kx) and y_(2) = 2a sin(omegat - kx) . The total mechanical energy confined between the sections corresponding to the adjacent antinodes is
View SolutionFrom a single source, two wave trains are sent in two different string. The two wave equations are ((area of cross-section and tension of both string are same y_(1) = A sin ( w_(1)t-k_(1)x)and y_(2) = 2A sin (w_(1)t -k_(2)z) Suppose u = energy density , P = power trasmitted and I = intensity of the wave, then match the following.
View SolutionLet the two waves y_(1) = A sin ( kx - omega t) and y_(2) = A sin ( kx + omega t) from a standing wave on a string . Now if an additional phase difference of phi is created between two waves , then
View Solutionदोनों सिरों से बँधी हुई डोरी पर अप्रगामी तरंग बनती है | व्यक्तिगत तरंगें : जैसे-आपतित तरंग एवं परावर्तित तरंग
y1(x,t)=asin(kx−ωt) एवं y2(x,t)=asin(kx+ωt) हैं | दोनों तरंगों की तरंगदैर्घ्य समान (λ) है |
निस्पन्दो की स्थिति दी जाती है
View Solutionदोनों सिरों से बँधी हुई डोरी पर अप्रगामी तरंग बनती है | व्यक्तिगत तरंगें : जैसे-आपतित तरंग एवं परावर्तित तरंग
y1(x,t)=asin(kx−ωt) एवं y2(x,t)=asin(kx+ωt) हैं | दोनों तरंगों की तरंगदैर्घ्य समान (λ) है |
प्रस्पंदो की स्थिति समीकरण दी जाती है
View Solutionदोनों सिरों से बँधी हुई डोरी पर अप्रगामी तरंग बनती है | व्यक्तिगत तरंगें : जैसे-आपतित तरंग एवं परावर्तित तरंग
y1(x,t)=asin(kx−ωt) एवं y2(x,t)=asin(kx+ωt) हैं | दोनों तरंगों की तरंगदैर्घ्य समान (λ) है |
दो क्रमागत प्रस्पंदो के बीच की दूरी है
View Solution

