If i=t2,0<t<T then r.m.s. value of current is
T2√2
T22
T2√5
none of these
The correct Answer is:C
To find the root mean square (RMS) value of the current given by the function i(t)=t2 for 0<t<T, we can follow these steps:
1. Understanding the RMS Formula:
The RMS value of a function i(t) over a period T is given by the formula:
Irms=√1T∫T0i2(t)dt
2. Substituting the Given Function:
Given i(t)=t2, we need to calculate i2(t):
i2(t)=(t2)2=t4
3. Setting Up the Integral:
Now, substitute i2(t) into the RMS formula:
Irms=√1T∫T0t4dt
4. Calculating the Integral:
We need to evaluate the integral ∫T0t4dt:
∫t4dt=t55
Now, apply the limits from 0 to T:
∫T0t4dt=(T55)T0=T55−0=T55
5. Substituting Back into the RMS Formula:
Now substitute the value of the integral back into the RMS formula:
Irms=√1T⋅T55=√T55T=√T45=T2√5
6. Final Result:
Thus, the RMS value of the current is:
Irms=T2√5
Summary:
The RMS value of the current i(t)=t2 over the interval 0<t<T is T2√5.
---
The RMS value of a function i(t) over a period T is given by the formula:
Irms=√1T∫T0i2(t)dt
Given i(t)=t2, we need to calculate i2(t):
i2(t)=(t2)2=t4
Now, substitute i2(t) into the RMS formula:
Irms=√1T∫T0t4dt
We need to evaluate the integral ∫T0t4dt:
∫t4dt=t55
Now, apply the limits from 0 to T:
∫T0t4dt=(T55)T0=T55−0=T55
Now substitute the value of the integral back into the RMS formula:
Irms=√1T⋅T55=√T55T=√T45=T2√5
Thus, the RMS value of the current is:
Irms=T2√5
The RMS value of the current i(t)=t2 over the interval 0<t<T is T2√5.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Comphension Based
8 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Archives Integer
1 Video
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
In a certain circuit current changes with time accroding to i=2√t. r.m.s. value of current between t=2 to t=4s will be
View SolutionIn the circuit shows in Fig. the initail current through the inductor at t=0 is I0. After a time t=L/R, the switch is quickly shifted to position 2.
a. Plot a graph showing the variation of current with time.
b. Calculate the value of current in the inductor at t=32LR.
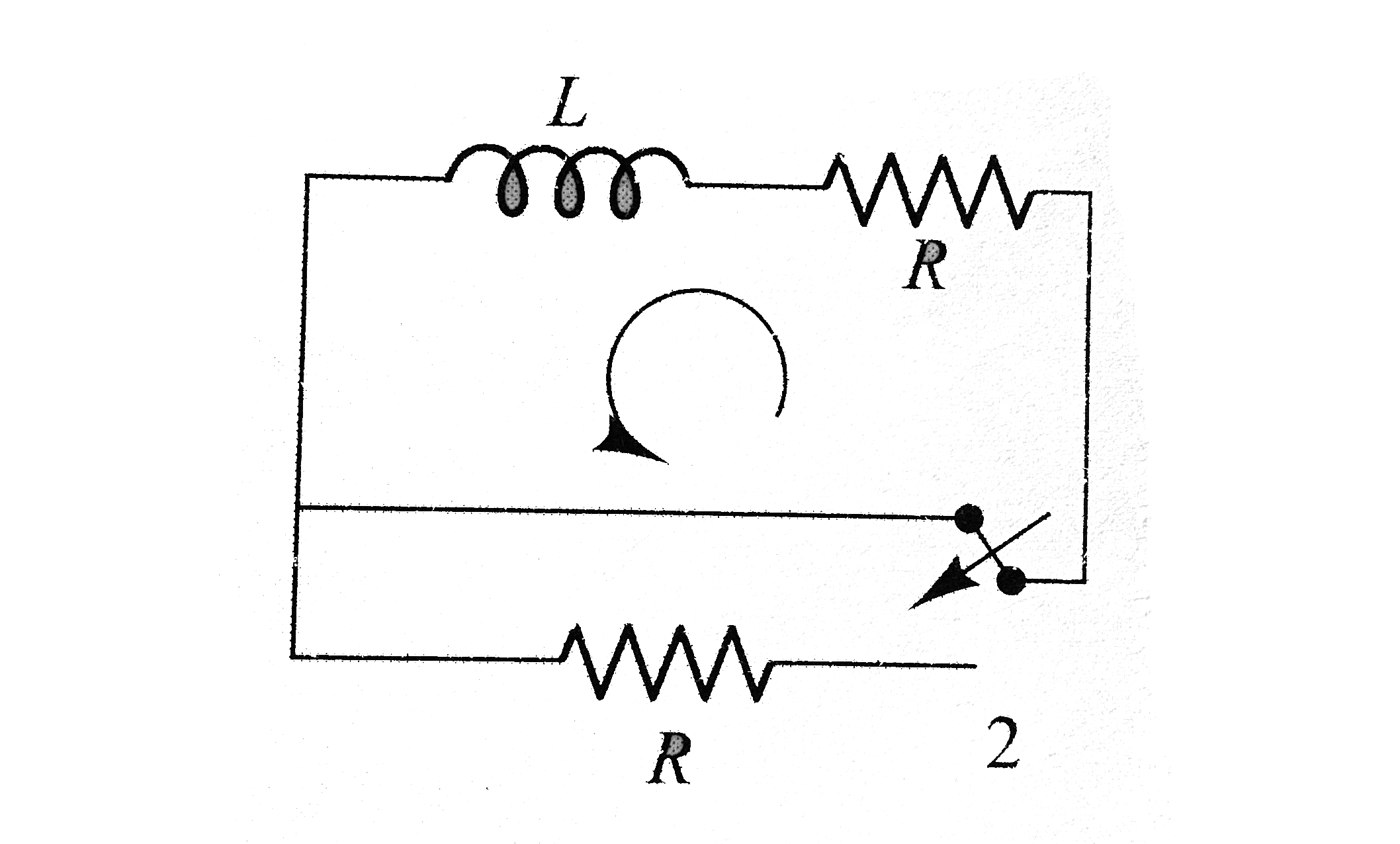
View SolutionCurrent in an ac circuit is given by i=2√2sin[(πt+((π)/4)]. Then find the average value of current during time t=0 to t=1 s.
View SolutionCurrent in an ac circuit is given by i=2√2sin[(πt+((π)/4)]. Then find the average value of current during time t=0 to t=1 s.
View SolutionThe current is given by i=i0+i0 sin omega t then its r.m.s value will be
View Solutionr.m.s. value of current i=3+4sin(ωt+π/3) is:
View SolutionA current i0 is flowing through an L−R circuit of time constant t0. The source of the current is switched off at time t=0. Let r be the value of (−di/dt) at time t=0.Assuming this rate to be constant, the current will reduce to zero in a time interval of
View SolutionThe electric curren in a charging R-C circuit is given by i=i0e−tRC when i0, R and C aere constant parameters of the circuit and t is time. Find the rate of change of current at a.t=0,b.t=RCc.t=10RC.
View SolutionThe voltage supplied to a circuit is given by V=V0t32, where t is time in second. Find the rms value of voltage for the period, t=0 to t=1s.
View SolutionThe electric current in a discharging R-C circuit is given by i=i0e−tRC where i0 Rand Care constant parameters and tis time. Let i0=2.00A, R=6.00×105ohm and C=0.500μF.
a. Find the current at t=0.3 s.
b. Find the rate of change of current at t=0.3 s.
Find approximately the current at t=0.31 s.
View Solution

