If random error in the arithmetic mean of 100 observations is x, then the randow error in the arithmetic mean of 500 observations would be
5x
x/5
25x
x/25
The correct Answer is:(b)
To solve the problem, we need to understand how random errors in the arithmetic mean change with the number of observations. The random error in the arithmetic mean decreases as the number of observations increases.
1. Understanding Random Error: The random error in the arithmetic mean is inversely proportional to the square root of the number of observations. This means that as we increase the number of observations, the random error decreases.
2. Formula for Random Error: The formula for the random error (E) in the arithmetic mean based on the number of observations (n) is given by:
E∝1√n
This implies that if we have a random error x for n=100, we can express it as:
E100=k√100=k10=x
where k is a constant.
3. Finding the Random Error for 500 Observations: Now, we need to find the random error when the number of observations is increased to 500. Using the same formula:
E500=k√500
4. Relating the Two Errors: We can relate E500 to E100:
E500=k√500=k√100×5=k10√5=x√5
5. Final Expression: Thus, the random error in the arithmetic mean of 500 observations is:
E500=x√5
Conclusion:
The random error in the arithmetic mean of 500 observations would be x√5.
E∝1√n
This implies that if we have a random error x for n=100, we can express it as:
E100=k√100=k10=x
where k is a constant.
E500=k√500
E500=k√500=k√100×5=k10√5=x√5
E500=x√5
The random error in the arithmetic mean of 500 observations would be x√5.
Similar Questions
Knowledge Check
if the randon error in the arithmetic mean of 50 observations is α, then the random error in the arithmetic mean of 150 observations would be
AαB3αCα3D2αFind the arithmetic mean of:
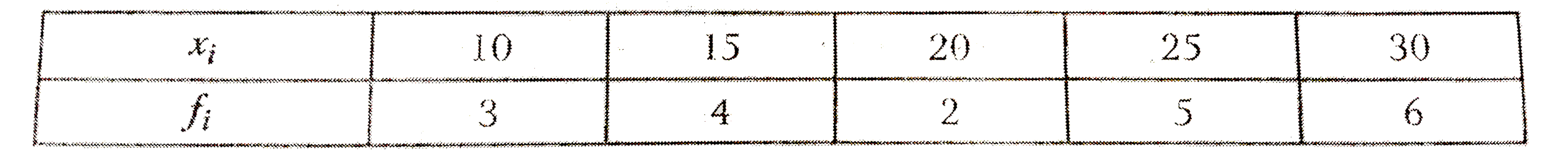 A21B21.4C22.75D21.75
A21B21.4C22.75D21.75Find the arithmetic mean of 4 and 12.
A9B8C16D10
Define Arithmetic mean.
View SolutionDefine Arithmetic mean.
View SolutionSimple Arithmetic Mean
View SolutionIf arithmetic mean of 9 observations is 100 and that of 6 is 80 .Then the combined mean of all the 15 observations will be
View SolutionIf arithmetic mean of 9 observations is 100 and that of 6 is 80 .Then the combined mean of all the 15 observations will be
View Solution
