In a double slit experiment, the distance between the slits is 5.0 mm and the slits are 1.0m from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480nm, and the other due to light with wavelength 600nm. What is the separation on the screen between the third order bright fringes of the two intergerence patterns?
The correct Answer is:[0.072 mm]
Step by step video, text & image solution for In a double slit experiment, the distance between the slits is 5.0 mm and the slits are 1.0m from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480nm, and the other due to light with wavelength 600nm. What is the separation on the screen between the third order bright fringes of the two intergerence patterns? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Numerical MCQs Single Options Correct
49 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.4
11 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Unsolved Numerical Problems for Preparation of NSE, INPhO & IPhO
135 Videos
Similar Questions
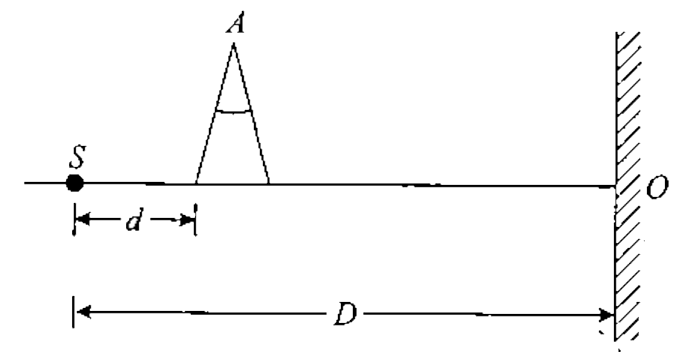
A prism having angle A∘ (which is very small) is placed in front of a point source S at a small distance d. A screen is placed at a large distance D as shown in the figure-6.113. Find the fringe width of interference pattern given that source is emitting light of wavelength λ and refractive index of prism is μ.
View SolutionIn Young's double-slit experiment the angular width of a fringe formed on a distant screen is 1∘. The wavelength of light used is 6000Å. What is the spacing between the slits?
View SolutionThe volume of one mode of an ideal gas with adiabatic exponent γ is varied according to the law V=a/T, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by ΔT.
View SolutionWrite down the equation of a wave travelling in the negative direaction along x-axis with an amplitude 0.01m, a frequency 550Hz and a speed 330m/s.
View SolutionIn a double slit experiment, the distance between the slits is 5.0 mm and the slits are 1.0m from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480nm, and the other due to light with wavelength 600nm. What is the separation on the screen between the third order bright fringes of the two intergerence patterns?
View SolutionCoherent light with wavelength 600nm passes through two very narrow slits and the interference pattern is observed on a screen 3.00 m from the slits. The first order bright fringe is at 4.94 mm from the centre of the central bright fringe. For what wavelength of light will the first order dark fringe be observed at this same point on the screen?
View SolutionIn a young's double slit experiment, two slits are illuminated by a mixture of two wavelength 12000Å and 10000Å . At 6.0 mm from the common central bright fringe on a screen 2 m away from the slits, a bright fringe of one interference pattern coincides with the bright fringe of other. Distance between the slits should by :
View SolutionMonochromatic light from a narrow slit illuminates two parallel slits producing an interference pattern on a screen. The separation between the two slits is now doubled and the distance between the screen and the slits is reduced to half. The fringe width
View SolutionIn Young's double slit experiment the two slits are d distance apart. Interference pattern is observed on a screen at a distance D from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is
View SolutionIn a Young's double slit experiment, the slits separated by 1 mm are illuminated by a mixture of two wavelengths λ=600nm and λ'=750nm. The distance of screen from slits is 1m. The minimum distance from the common central bright fringe where the bright frigne of one interference pattern will coincide with the bright fringe of second inteference pattern will be:
View SolutionInterference fringes are obtained in a Young's double slit experiment using beam of light consisting two wavelengths 500 nm and 600 nm. Bright fringes due to both wavelengths coincide at 2.5 mm from the central maximum. If the separation between the slits is 3 mm, then the distance between the screen and plane of the slits is
View SolutionInterference fringes are obtained in a Young's double slit experiment using beam of light consisting two wavelengths 500 nm and 600 nm. Bright fringes due to both wavelengths coincide at 2.5 mm from the central maximum. If the separation between the slits is 3 mm, then the distance between the screen and plane of the slits is
View SolutionIn a double slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480 nm, and the other due to light with wavelength 600 nm. What is the separation on the screen between the fifth order bright fringes of the two interference patterns?
View SolutionWhat is interference of light waves ? State two essential conditions to observe it.
In Young's double slit experiment, light of wavelength 6000⋅A is used to get an interference pattern on a screen. The fringe width changes by 1.5 mm when the screen is brought towards the double slit by 50 cm. Find the distance between the two slits.
View SolutionCalculate the distance between 5^(th) and 15^(th) bright fringes in an interference pattern obtained by experiment due to narrow slits separated by 0.2mm and illuminated by light of wavelength 560mm . The distance between the slit and screen is 1m .
View SolutionIn a Young's double slit experiment the separation between the slits is 0.10 mm, the wavelength of light used is 600 nm and the interference pattern is observed on a screen 1.0 m away. Find the separation between the successive bright fringes.
View Solution

