In an L-C -R series circuit connected to an AC source V=V0sin(100π(t)+π6)VR=40V,VL=40andVC=10V, resistance R=4Ω
peak value of current is
10√2A
15√2A
20√2A
25√2A
The correct Answer is:A
To find the peak value of current in the given L-C-R series circuit connected to an AC source, we can follow these steps:
Step 1: Understand the given values
We are given:
- VR=40V (Voltage across the resistor)
- VL=40V (Voltage across the inductor)
- VC=10V (Voltage across the capacitor)
- R=4Ω (Resistance)
- The AC voltage source is given by V=V0sin(100πt+π6).
Step 2: Calculate the RMS current using the voltage across the resistor
The voltage across the resistor VR is related to the RMS current IRMS by Ohm's law:
VR=IRMS⋅R
Substituting the known values:
40=IRMS⋅4
To find IRMS:
IRMS=404=10A
Step 3: Calculate the peak current
The peak current Ipeak can be calculated from the RMS current using the relationship:
Ipeak=IRMS⋅√2
Substituting the value of IRMS:
Ipeak=10⋅√2≈14.14A
Final Answer
The peak value of current is approximately 14.14A.
---
We are given:
- VR=40V (Voltage across the resistor)
- VL=40V (Voltage across the inductor)
- VC=10V (Voltage across the capacitor)
- R=4Ω (Resistance)
- The AC voltage source is given by V=V0sin(100πt+π6).
The voltage across the resistor VR is related to the RMS current IRMS by Ohm's law:
VR=IRMS⋅R
Substituting the known values:
40=IRMS⋅4
To find IRMS:
IRMS=404=10A
The peak current Ipeak can be calculated from the RMS current using the relationship:
Ipeak=IRMS⋅√2
Substituting the value of IRMS:
Ipeak=10⋅√2≈14.14A
The peak value of current is approximately 14.14A.
Similar Questions
Knowledge Check
In a series L-R circuit (L=35mHandR=11Ω), a variable emf source (V=V0sinωt) of Vrms=220V and frequency 50 Hz is applied. Find the current amplitude in the circuit and phase of current with respect to voltage. Draw current-time graph on given graph (π=227).
 A10AB20 AC30 AD40 A
A10AB20 AC30 AD40 A
Consider in L−C−R circuit as shown in figureure with an AC source of peak value V0 and angular frequency ω. Then the peak value of current through the AC
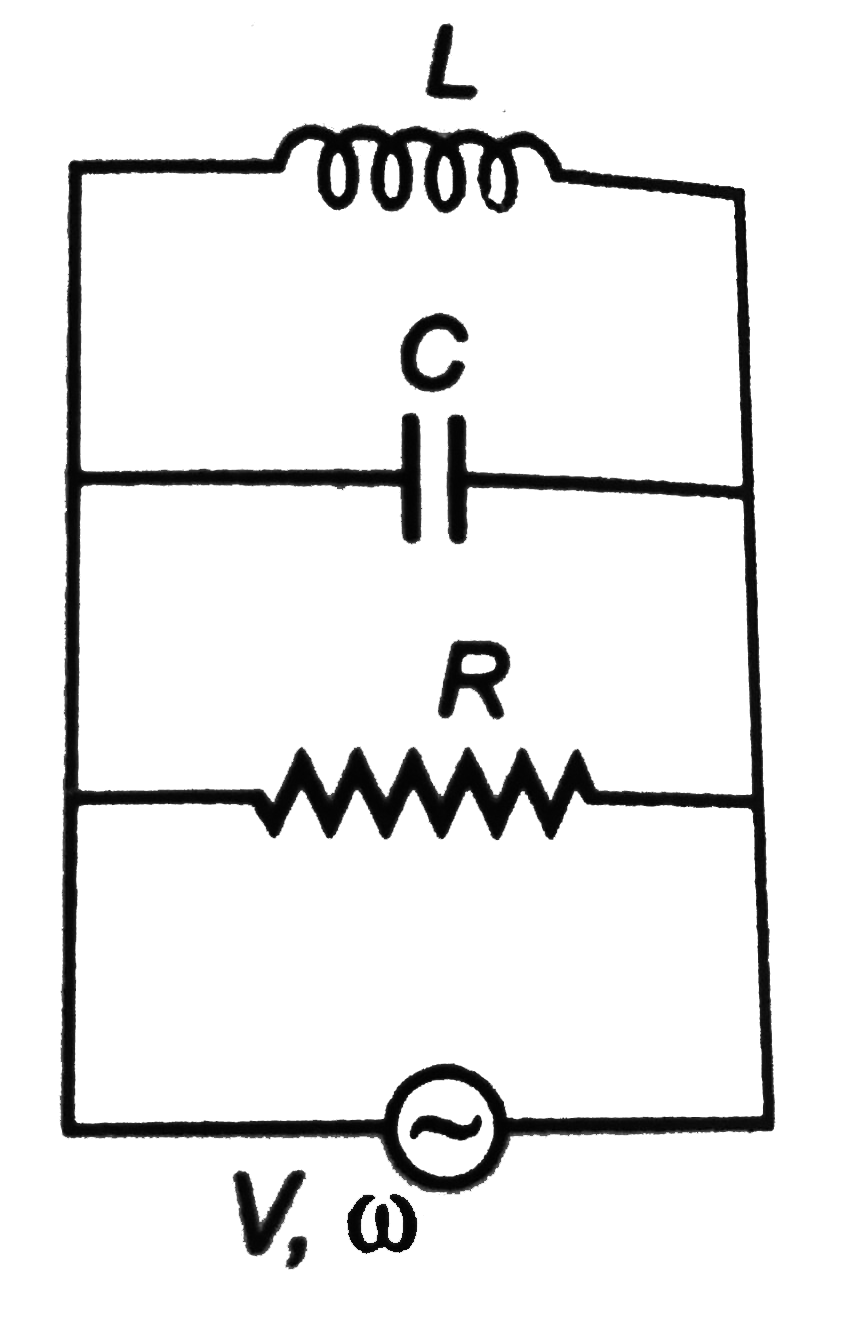 .
.
View SolutionResistor, inductor and capacitor are connected in parallel to an AC source of emf V=100sinωt If R=2Ω,XL=2ΩandXC=4Ω,, then choose correct option:

View SolutionIn an AC series L−C−R circuit, applied voltage is
V=(100√2sin(ωt+45∘))V
Given that, R=30Ω, XL=50Ω and XC=10Ω Now match the following two columns.

View SolutionAn LCR series circuit with L=100mH,C=100μF,R=120Ω is connected to an AC source of emfε=(30V)sin(100s−1)t. Find the impedane, the peak current and the resonant frequency of the circuit.
View SolutionA series L-C-R circuit is connected across an AC source V = 10sin[100πt−π6]. Current from the supply is I = 2sin[100πt+π12], What is the average power dissipated?
View SolutionA series L-C-R circuit is connected across a variable frequency source of emf. VL,VC,VR are instantaneous voltage drops across inductor capacitor and resistor and V is instantaneous voltage across the circuit.
Column I Column II(A)|V|(p)Can be greater than zero(B)|V|−|VL|(q)Can be less than zero(C)|V|−|VC|(r)Can be equal to zero(D)|V|−|VR|
View SolutionIn a series LCR circuit, the the rms voltage supply is 170 V. If VR,VLandVC represent the rms voltage drop across resistor , inductor and capacitor, then
View Solution

