In Fresnel's biprism (μ=1.5) experiment the distance between source and biprism is 0.3m and that between biprism and screen is 0.7m and angle of prism is 1∘. The fringe width with light of wavelength 6000Å will be
3 mm
0.11 mm
2 mm
4 mm
Step by step video solution for In Fresnel's biprism (mu=1.5) experiment the distance between source and biprism is 0.3m and that between biprism and screen is 0.7m and angle of prism is 1^@. The fringe width with light of wavelength 6000Å will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A musician using and open flute of length 50 cm produces second harmonic sound waves. A person runs towards the musician from another end of a hall at a speed of 10 km/h. If the wave speed is 330 m/s, the frequency heard by the running person shall be close to :
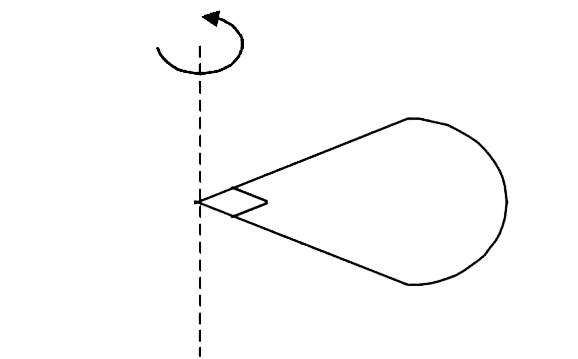
View SolutionOne quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. it is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is
View SolutionIn Fresnel's biprism (mu=1.5) experiment the distance between source and biprism is 0.3m and that between biprism and screen is 0.7m and angle of prism is 1^@ . The fringe width with light of wavelength 6000Å will be
View SolutionIf prism angle alpha=1^@ , mu=1.54 , distance between screen and prism (b)=0.7m , distance between prism and source a=0.3m , lambda=180pi nm then in Fresnel biprism find the value of beta (fringe width).
View SolutionIn Fresnel's biprism experiment, on increasing the prism angle, the fringe width will
View SolutionIn fresnel's biprism experiment the distance between the source and the screen is 1 ma nd that between the screen is 1 m and that between the source and biprism is 10 cm. the wavelength of light used is 6000Å. The fringe width obtained is 0.03 cm and the refracting angle of biprism is 1^(@) then calculate the refractive index of the material of biprism.
View SolutionIn a Fresnel's biprism experiment, sodium light of wavelength 5832 Å is used. Calculated the fringe width, given the distance between the screen and the biprism =120 cm and the distance the two sources=0.04 cm.
View SolutionThe distance between the slit and the biprism and between the biprims and the screen 50 cm each. The angle of the biprism is 179^(@) and its refractive index is 1.5 . If the distance between successive bright fringes is 0.0135 cm , then the wavelenghts of lights is
View SolutionThe obtuse angle of Fresnel's biprism is 178∘. A slit is illuminated by light to wavelenght 6000Å is at distance of 10 cm from the biprism. Find the fringe widht on a screen at a distance of 90 cm from the biprism . The refractive index of the material of the birism is 1.5
View SolutionIn Fresnel's biprism experiment, when the distance between the slit aperture and eye is increased, then distance between the fringes
View SolutionIf the wavelength of light is kept constant and the biprism is moved towards the screen, then the fringe width
View SolutionA fresnel biprism is used to form the inerference fringes. The distance between the source and the biprisim is 20 cm and that between the biprism and the screen is 80 cm. If A= 6563 A and the separation between the virtual sources is 3.6 mm, then the fringes width (in mm) is.
View SolutionIn a biprism experiment the distance of source from biprism is 1 m and the distance of screen from biprism is 4 meters. The angle of refraction of biprism is 2xx10^(-3) radians. mu of biprism is 1.5 and the wavelength of light used is 6000 Å. How many fringes will be seen on the screen ?
View SolutionIn Fresnel’s biprism experiment if the screen is moved away from the biprism, then the fringe width will :
View SolutionA Fresnel's biprism is used to form the interference fringes. The distance between the source and the biprism is 20 cms and that between the biprism and the screen is 80 cm. If lambda=6563 Å and the separation between the virtual sources is 3.6 mm, then the fringe width is :
View SolutionA Fresnel's biprism is used to form the interference fringes.The distance between the source and the biprism is 20 cms and that between the biprism and the screen is 80 cm. If lambda = 6563 Å and the separation between the virtual sources is 3.6 mm, then the fringe width is :
View Solution
