In the arrangement shown in figure, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed. Mass M moves upwards with a speed
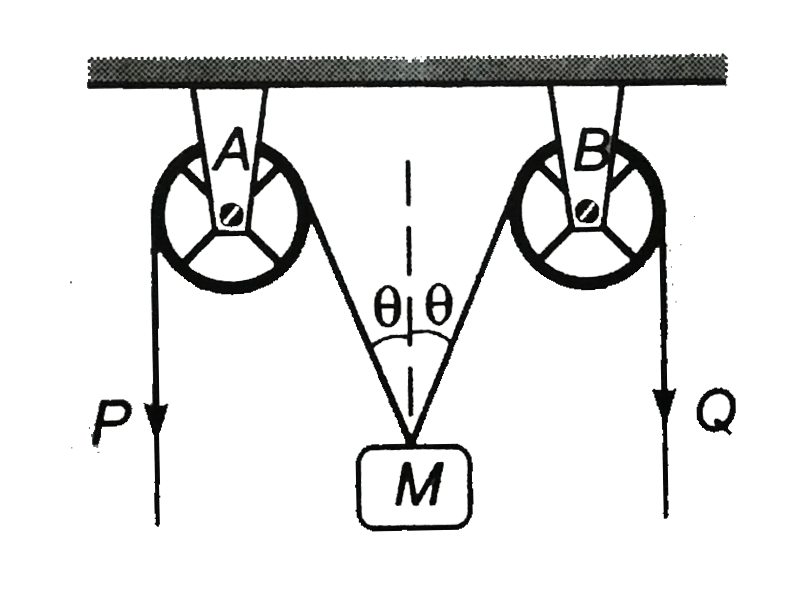
(a) 2Ucosθ (b) Ucosθ (c) 2Ucosθ (d) Ucosθ
The correct Answer is:False
For mass m
T−mg=ma….(i)
For mass 2m
2mg−T−2ma….(ii)
From(i) and (ii) a=g/3
In second caseT−mg=ma'
2mg−mg=ma'
a'=g

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Single correct answer type
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple correct answer type
Explore 3 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer
Explore 6 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
In the arrangement shown in figure, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed. Mass M moves upwards with a speed

(a) 2Ucosθ (b) Ucosθ (c) 2Ucosθ (d) Ucosθ
View SolutionIn the arrangement shown in the Fig, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed.
Mass M moves upwards with a speed
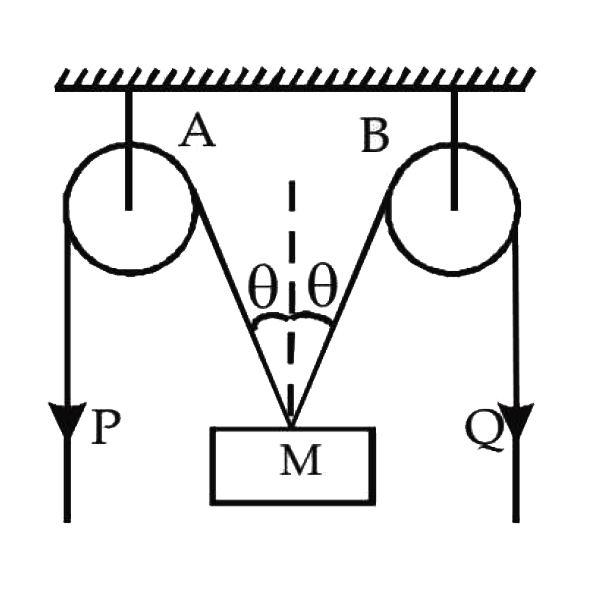
View Solution
Knowledge Check
In the arrangement shown in Fig. 15.3.15 the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A nd B are fixed. Mass M moves upwards with a speed.
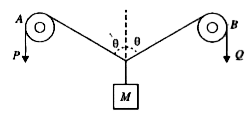 A2 U cosθBU cosθC2 U/cosθDU/cosθ
A2 U cosθBU cosθC2 U/cosθDU/cosθ
In the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed

View Solution∫dθ(sinθ−2cosθ)(2sinθ+cosθ)
View Solution∫d(cosθ)√1−cos2θ
View Solutionlf cos5θ−acos5θ+bcos3θ+ccosθ then c is equal to-
View SolutionThe value of cos4θ+sin4θ−6cos2θ is (a) cos2θ (b) sin2θ (c) cos4θ (d) none of these
View Solutionifacosθ+bsinθ=c. then what is the value of asinθ−bcosθ
View SolutionEvaluate: ∫cos2θln(cosθ+sinθcosθ−sinθ)dθ
View Solution
