In the figure shown mass of both the spool and block is m moment of inertia of the spool about centre of mass is 2mR2 the spools rolls on horizontal surface there is no slipping at any surfaces in contact the ratio of kinetic energy of the spool to that of block is
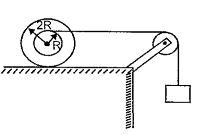
(3/4)
(1/3)
(2/3)
(1/2)
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
The dimensional formula for the modulus of elasticity is same as that for
View SolutionA simple harmonic oscillation is represented by , x = 0.40 sin (440t + 0.61)
Here, x and t are in m and s respectively find amplitude
View Solution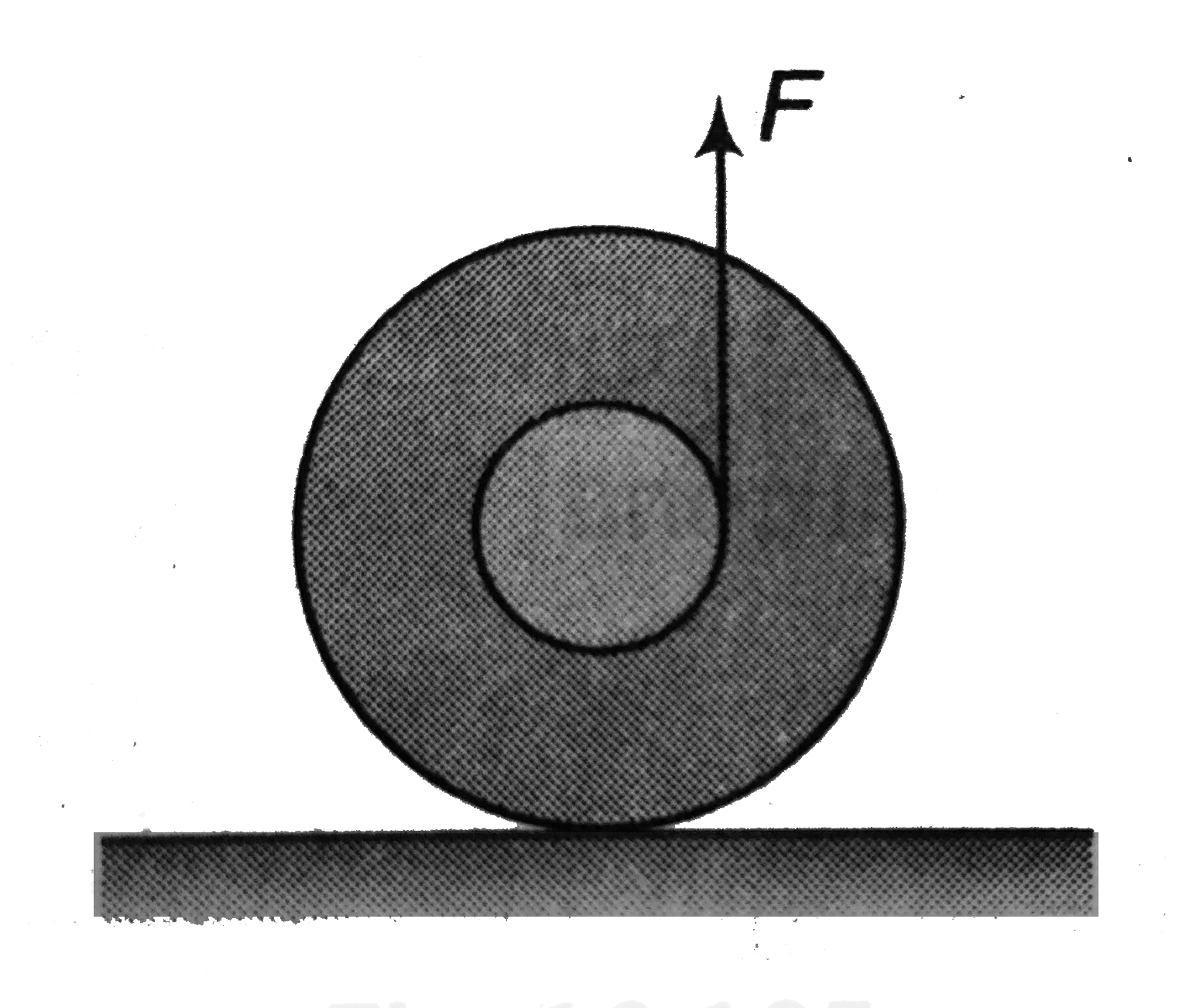
A spool is pulled by a force in vertical direction as shown in figure . What is the direction of friction in this case? The spool does not loose contact with the ground.
View SolutionA spool is pulled at an angle theta with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle theta is equal to
View SolutionIn the figure shown mass of both, the spherical body and block is m . Moment of inertia of the spherical body about centre of mass is 2mR^(2) . The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
View SolutionConsider an arrangement shown in the figure. The pulley P is frictionless and the threads are massless. The mass of the spools is m and moment of inertia of the spool is 12mR2. The mass of the disc of radius R is also m. The surface below the spool is rough to ensure pure rolling of spool. the mass of the block is m and the surface below the block is smooth. find the initial acceleration of the block when the system is released from rest.

View SolutionA spool has the shape shown in figure. Radii of inner and outer cylinders are R and 2 R respectively. Mass of the spool is 3 m and its moment of inertia about the shown axis is 2 m R^(2) . Light threads are tightly wrapped on both the cylindrical parts. The spool is placed on a rough surface with two masses m_(1) = m and m_(2) = 2m connected to the strings as shown. The string segment between spool and the pulleys P_(1) and P_(2) are horizontal. The centre of mass of the spool is at its geometrical centre. System is released from rest. (a) What is minimum value of coefficient of friction between the spool and the table so that it does not slip? (b) Find the speed of m_(1) when the spool completes one rotation about its centre.
View SolutionA spool of mass m has moment of inertia I= 2mR^(2) about its axis of symmetry. The inner and outer radius of spool R and 2R respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle theta with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface. For theta=0^(@) , the acceletation of spool is
View SolutionA spool of mass m has moment of inertia I= 2mR^(2) about its axis of symmetry. The inner and outer radius of spool R and 2R respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle theta with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface. For theta=60^(@) the acceleration of spool is
View SolutionA spool of mass m has moment of inertia I=2mR2 about its axis of symmetry. The inner and outer radius of spool R and 2R respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle θ with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Regarding to the direction of rotation of spool which of the following statement is true?
View SolutionA spool of mass m has moment of inertia I=2mR2 about its axis of symmetry. The inner and outer radius of spool R and 2R respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle θ with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Maximum frictional force acting on the spool is:
View SolutionIn the figure shon mass of both, the spherical body and blocks is m. Moment of inertia of the spherical body about centre of mass is 2mR^(2) . The spherical body rolls on the horizontal surface. There is no sliiping between any two surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
View SolutionA spool of wire rests on a horizontal surface as shown in figure. As the wire is pulled, the spool does not slip at contact point P. On separate trials, each one of the force F1,F2,F3 and F4 is applied to the spool. For each one of these forces the spool.
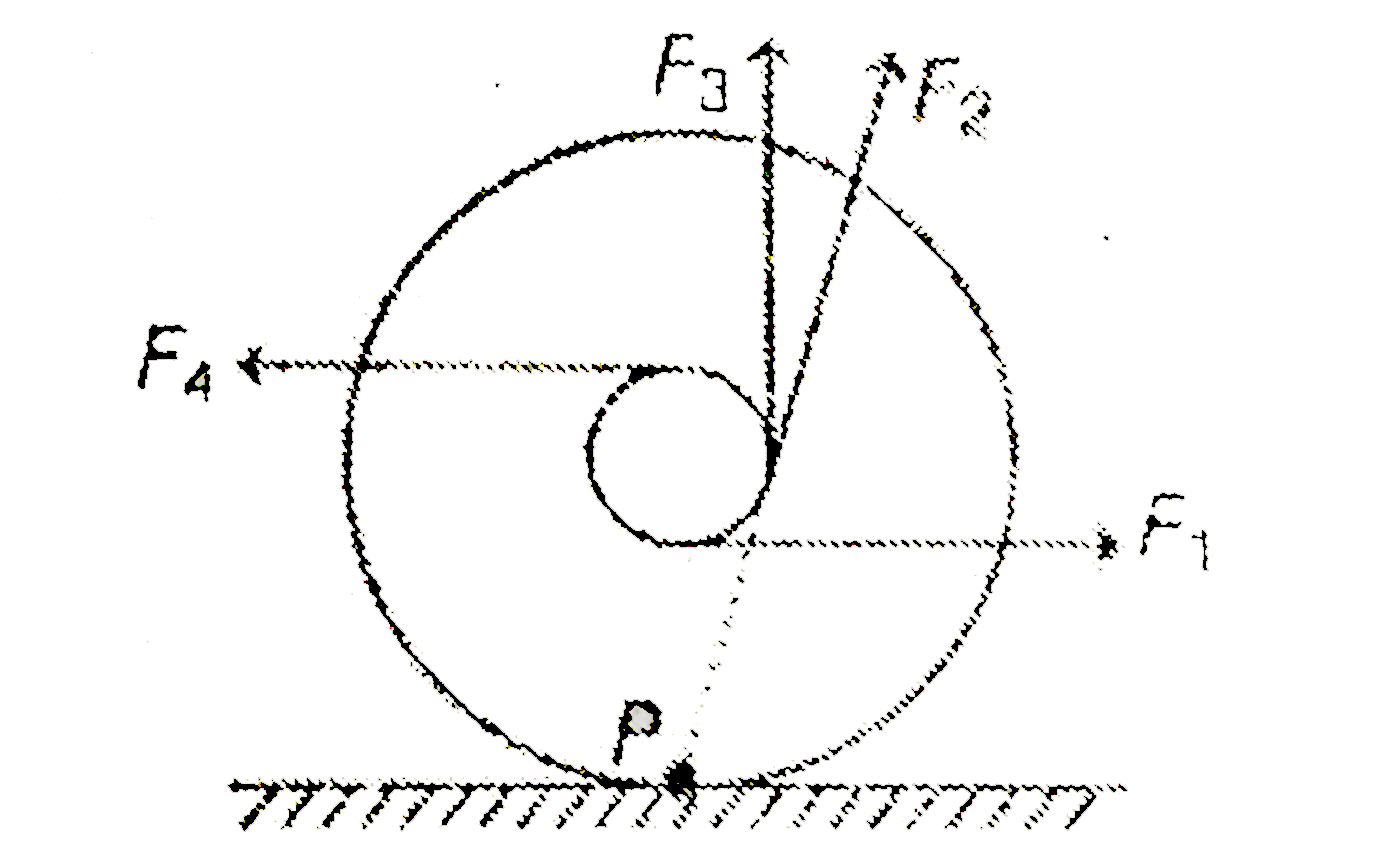
View SolutionA spool of wire rests on a horizontal surface as shown in figure. As the wire is pulled, the spool does not slip at contact point P. On separate trials, each one of the forces F1,F2,F3 and F4 is applied to the spool. For each one of these forces the spool
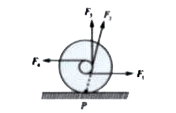
View SolutionPassage - II In th diagram a block of mass m is connected to a spool of mass 3m, inner radius R and outer radius 2R as shown. If pulley is light and surface is sufficiently rough such that no sliding place. Let moment of inertia of spool is mR^(2) , about the axis passing through through centre of mass and perpendicular to plane of rotation. The system is released from rest, answer the following The acceleration of the block and angular acceleration of spool is
View SolutionPassage - II In th diagram a block of mass m is connected to a spool of mass 3m, inner radius R and outer radius 2R as shown. If pulley is light and surface is sufficiently rough such that no sliding place. Let moment of inertia of spool is mR2, about the axis passing through through centre of mass and perpendicular to plane of rotation. The system is released from rest, answer the following

When the block falls down by a distance x the angular speed of spool is
View Solution

