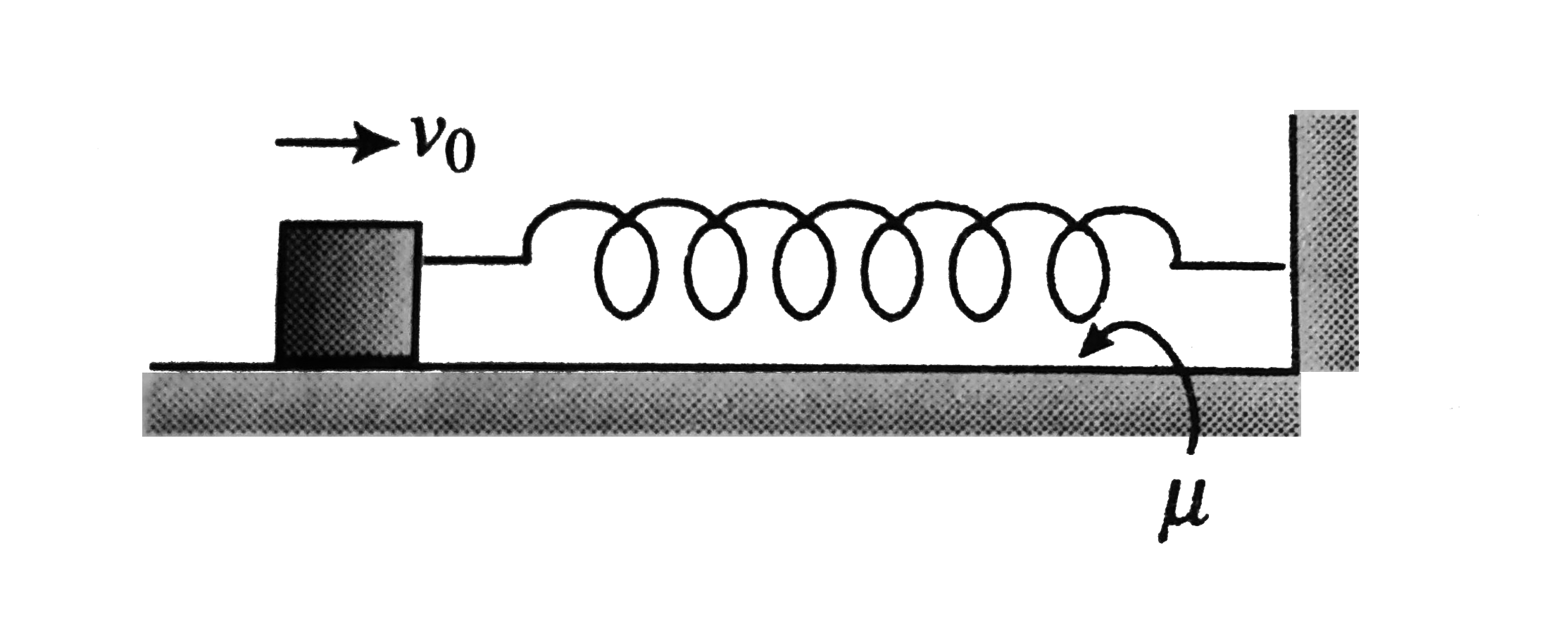
In the position shown in figure, the spring is at its natural length. The block of mass m is given a velocity v0 towards the vertical support at t=0. The coefficient of friction between the block and the surface is given by μ=αx, where α is a positive constant and x is the position of the block from its starting position. The block comes to rest for the first time at x, which is
(a) v0√mk+αmg
(b) v0√mk
(c) v0√mαg
(d) None of these
The correct Answer is:A
According to the work-energy theorem,
12mv20=mgαx∫0dx+12kx2
Solving we get, x=v0√mk+αmg
Similar Questions
A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA small block of mass 1 kg is at rest on a parabolic surface given by y=x2. The coefficient of friction between the block and the surface is enough to prevent slipping. If position of block on surface is (2 m, 4 m), then the normal force that the surface exerts at this position is
_PHY_E05_190_Q04.png)
View Solution
Knowledge Check
A block of mass 0.18 kg is attached to a spring of force constant 2N/m. The coefficient of friction between the block and the floor is 0.1. Initially, the block is at rest and the spring is unstretched. An impulse is given to the block.
The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is v=N/10. Then, N isA2B3C4D6A block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
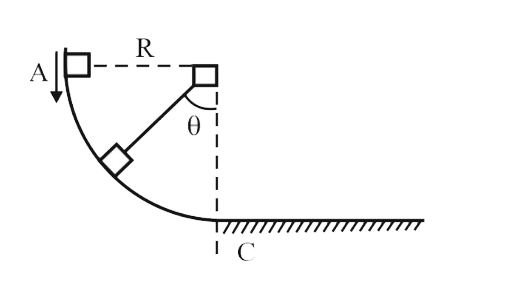 Aμ=sinθcotθ+v2RgBμ=sinθcosθ+v2RgCμ=tanθcosθ+v2RgDμ=cosθtanθ+v2Rg
Aμ=sinθcotθ+v2RgBμ=sinθcosθ+v2RgCμ=tanθcosθ+v2RgDμ=cosθtanθ+v2RgA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
AμB3μ2C2μD5μ2
A plank of mass M and length L is placed at rest on a smooth horizontal surface A small block of mass m is projected wii:h a velocity v0 as shown in the Fig. 3.31 (a), The coefficient of friction between the block and the plank is μ, plank is very long so that block eventually comes to rest on it.
(i) Find the work done by the ftjctioh force on the block during the period it slides on the plank. Is the Work positive or negative ?'
(ii) Calculate the work done on the plank during the same period. Is the work positive or negative?
(iii) Also, determine the net work done by friction. Is it positive or negative ?

View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View Solution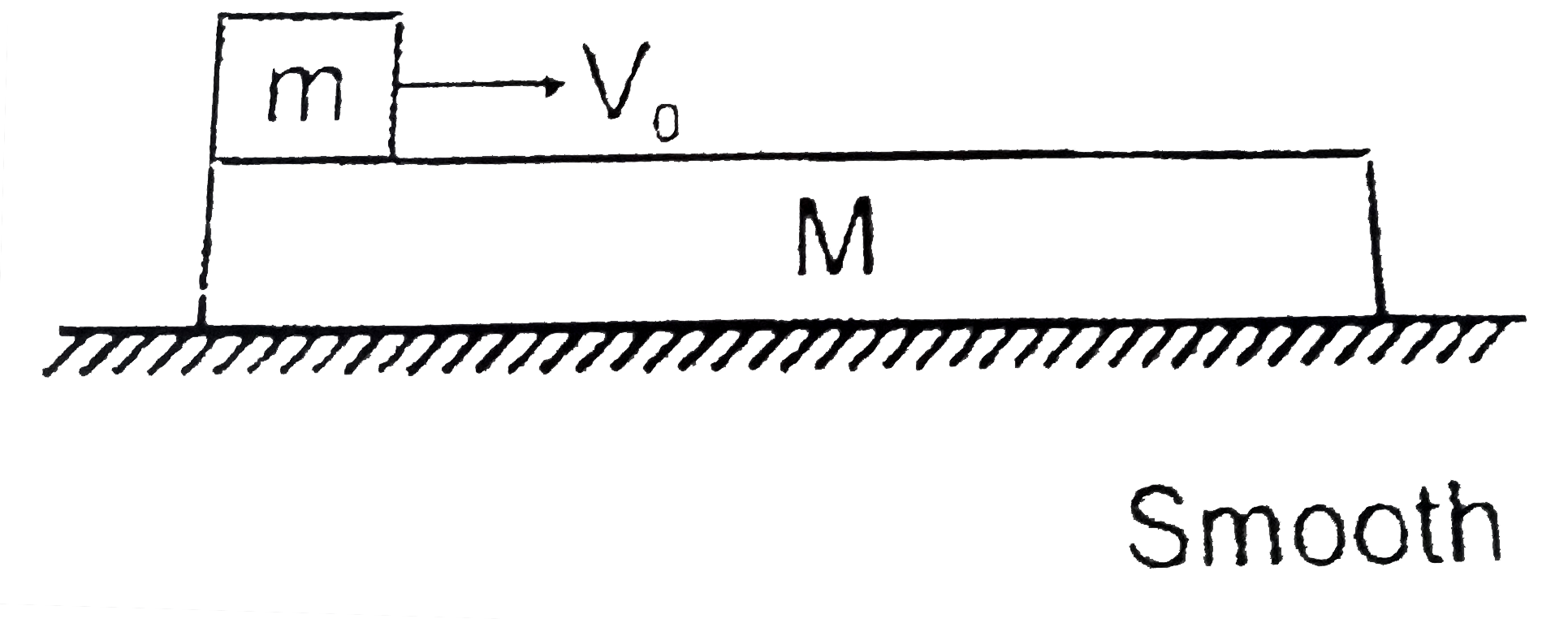
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
View SolutionA block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
View Solution
