In the third normal mode of vibrationn of a closed organ pipe, the number of nodes and antinodes respectively are
4,3
3,4
3,3
4,4
The correct Answer is:C
To solve the problem of determining the number of nodes and antinodes in the third normal mode of vibration of a closed organ pipe, we can follow these steps:
Step 1: Understand the structure of a closed organ pipe
A closed organ pipe has one end closed (node) and the other end open (antinode). The closed end will always have a node, where the displacement of air is zero, while the open end will have an antinode, where the displacement is maximum.
Hint: Remember that closed ends have nodes and open ends have antinodes.
Step 2: Identify the normal modes of vibration
In a closed organ pipe, the normal modes of vibration can be represented as follows:
- The first normal mode (fundamental frequency) has 1 node (at the closed end) and 1 antinode (at the open end).
- The second normal mode has 2 nodes and 1 antinode.
- The third normal mode has 3 nodes and 2 antinodes.
Hint: Each successive normal mode adds one additional node and one additional antinode.
Step 3: Analyze the third normal mode
In the third normal mode of vibration:
- The closed end still has 1 node.
- There will be additional nodes along the length of the pipe. For the third mode, we will have a total of 3 nodes.
- The open end will have 1 antinode, and there will be additional antinodes in between. For the third mode, we will have a total of 3 antinodes.
Hint: Count the nodes and antinodes carefully in the diagram of the third normal mode.
Step 4: Conclusion
From the analysis, we conclude that in the third normal mode of vibration of a closed organ pipe, there are:
- Number of nodes: 3
- Number of antinodes: 2
Thus, the answer is:
- Nodes: 3
- Antinodes: 2
Final Answer
The number of nodes and antinodes in the third normal mode of vibration of a closed organ pipe are 3 and 2, respectively.
---
A closed organ pipe has one end closed (node) and the other end open (antinode). The closed end will always have a node, where the displacement of air is zero, while the open end will have an antinode, where the displacement is maximum.
In a closed organ pipe, the normal modes of vibration can be represented as follows:
- The first normal mode (fundamental frequency) has 1 node (at the closed end) and 1 antinode (at the open end).
- The second normal mode has 2 nodes and 1 antinode.
- The third normal mode has 3 nodes and 2 antinodes.
In the third normal mode of vibration:
- The closed end still has 1 node.
- There will be additional nodes along the length of the pipe. For the third mode, we will have a total of 3 nodes.
- The open end will have 1 antinode, and there will be additional antinodes in between. For the third mode, we will have a total of 3 antinodes.
From the analysis, we conclude that in the third normal mode of vibration of a closed organ pipe, there are:
- Number of nodes: 3
- Number of antinodes: 2
- Nodes: 3
- Antinodes: 2
The number of nodes and antinodes in the third normal mode of vibration of a closed organ pipe are 3 and 2, respectively.
Similar Questions
Knowledge Check
In closed organ pipe at one end-
 AA-T,B-P,C-P,D-TBA-S,B-P,C-P,D-(Q,T)CA-S,B_Q,C-R,D-QDA-R,B_Q,C-S,D-(Q,T)
AA-T,B-P,C-P,D-TBA-S,B-P,C-P,D-(Q,T)CA-S,B_Q,C-R,D-QDA-R,B_Q,C-S,D-(Q,T)Modes of vibration in a closed organ pipe are represented by –
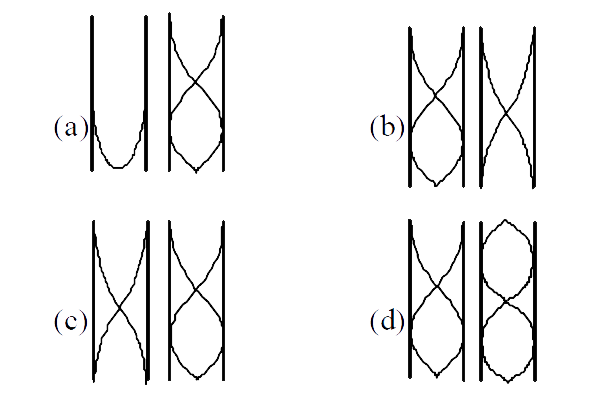 AaBbCcDd
AaBbCcDdIn the fundamental mode of vibration on a stretched string, the number of antinodes are
AOneBTwoCThreeDNone
Assertion : In the nth normal mode of vibration of a string, there are (n+1) nodes and n antinodes.
Reason : This is because both the ends of the string are fixed and from nodes.
View SolutionIn the 5th overtone of an open organ pipe, these are (N-stands for nodes and A- for antinodes)
View SolutionModes of vibration in an open organ pipe are represented by –
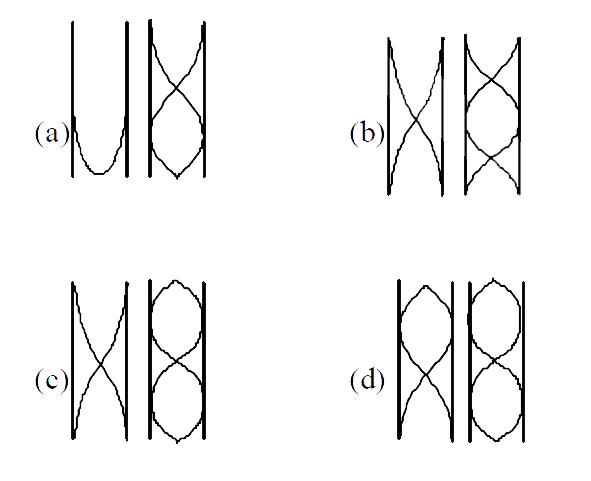
View SolutionA closed organ pipe emits harmonics in the ratio of
View SolutionEnd correction in a closed organ pipe of diameter 'd' is
View Solution


