In YDSE, light of wavelength λ=5000Å is used, which emerges in phase from two a slits distance d=3×10−7m apart. A transparent sheet of thickness t=1.5×10(−7)m, refractive indes n=1.17, is placed over one of the slits. Where does the central maxima of the interference now appear from the center of the screen? (Find the value of y?)
D(μ−1)t2d
2D(μ−1)td
D(μ+1)td
D(μ−1)td
The correct Answer is:d
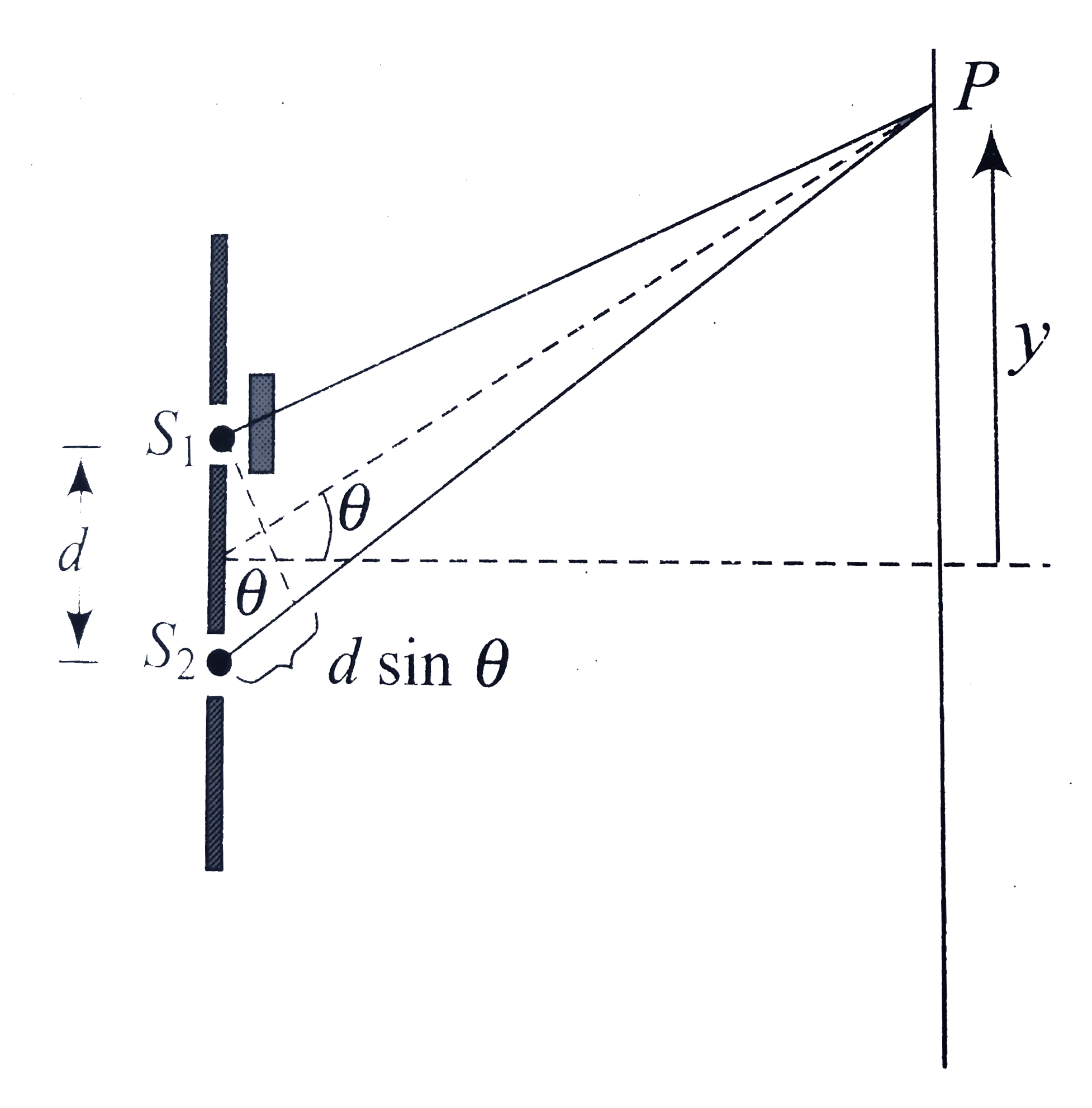
The path difference intorduced due to introduction of transparent sheet is given by Δx=(m−1)t.
If the central maxima occupies position of nth fringe, then
(μ−1)t=nλ=dsinθ
⇒sinθ(μ−1)td=(1.17−1)×1.5×10−73×10−7
=0.085
Hence, the angular position of central maxima is
θ=sin−1(0.085)=4.88∘
For small angles,
sinθ=θ=tanθ
⇒tanθ=yD
∴yD=(μ−1)td
Shift of central maxima is
y=D(μ−1)td
This formula can be used if D is given.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In Young's double-slit experiment, two wavelengths of light are used simultaneously where λ2=2λ1. In the fringe pattern observed on the screen,
View SolutionStatement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zero
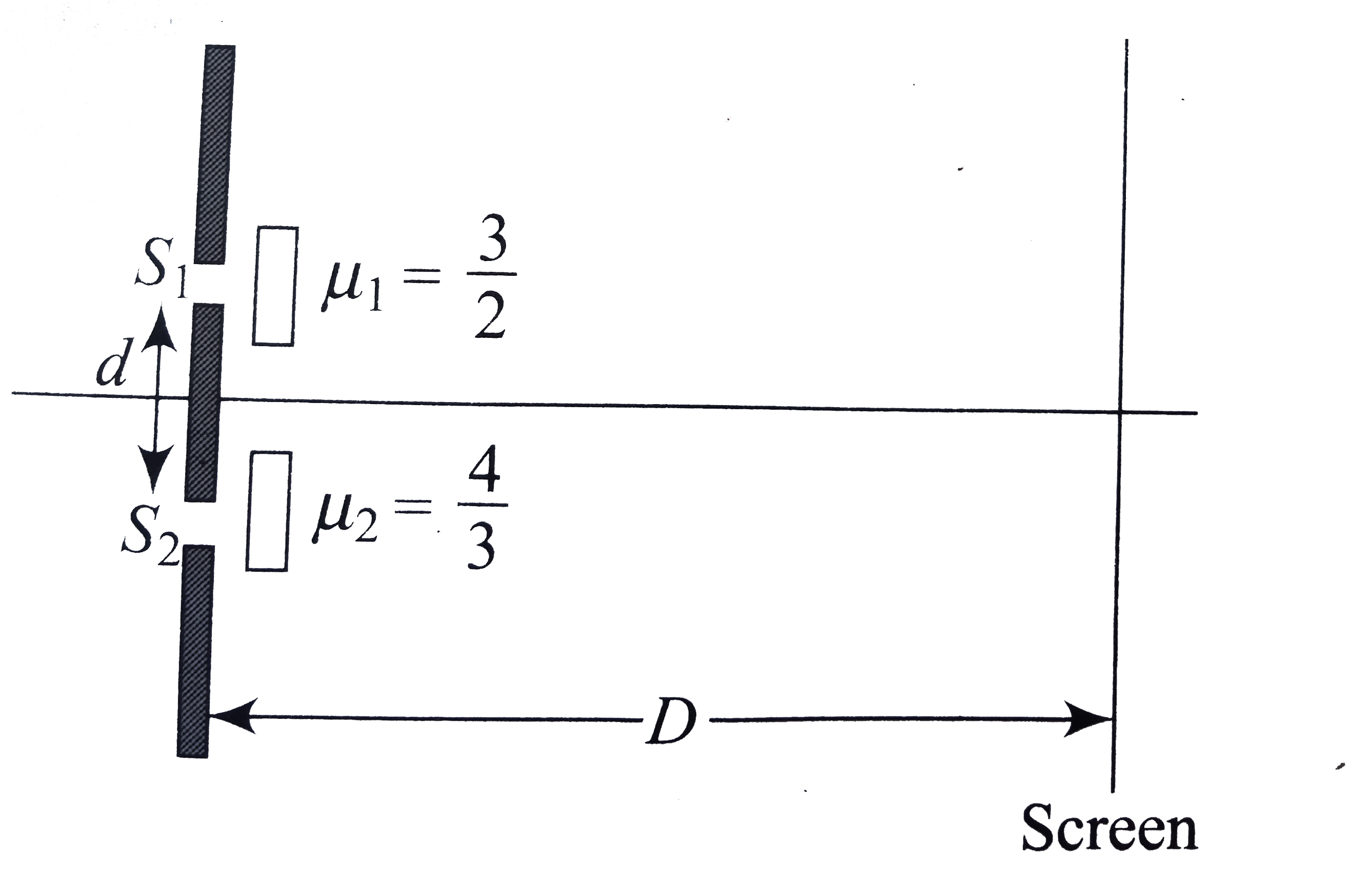
View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
View SolutionThree distinct current wires intersect a finite rectangular plane ABCD. The current is left wire and the loop is l1 . The direction of current in left most wire and righy most loop is downards as shown in the figure. The current l2through middle wire is adjusted so that the path integal of the total magnetic field along the perimeter of the rectangle is zero , that is ,∮ABCDA→B.d→s=0 then the current I2 is

View SolutionIn YDSE, the two slits are separated by 0.1 mm and they are
0.5 m from the screen. The wavelength of light used is 5000 Å. Find the distance
between 7th maxima and 11 th mimima on the upper side of screen.
View SolutionA monochromatic light of λ=500Å is incident on two identical slits separated by a distance of 5×10−4 m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness 1.5×10−6 m and refractive index μ=1.5 is placed between one of the slits and the screen . Find the intensity at the center of the screen.
View SolutionIn YDSE, light of wavelength λ=5000Å is used, which emerges in phase from two a slits distance d=3×10−7m apart. A transparent sheet of thickness t=1.5×106(−7)m, refractive indes n=1.17, is placed over one of the slits. Where does the central maxima of the interference now appear from the center of the screen? (Find the value of y?)

View SolutionIn YDSE with monochromatic light, fringes are obtained on the screen placed at some distance from the slits. If screen is moved by 5×10–2m towards the slits, fringe width changes by 3×10−5m. If separation between the slits is 10–3 m, if wavelength of light used is 1000 y Å, then y is : (Assume distance between the two slits is very small than the distance betwen the slits and screen)
View SolutionIn a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe.the intensity at a distance x=4×10−5in form the central maximum is-
View SolutionIn Young's double slit experiment with monochromatic light interference fringe are obtained on a screen placed at some distance from the slits. If the screen is moved by 5×10−2 m towards the slit the change in fringe width is 3×10−5 m. If the distance between the slits is 10−3 m the wavelength of the used is
View SolutionThe fringe width in Young's double slit experiment on a screen which is placed at a distance of 1 m from the slits 10^(-3) m apart when the light used has wavelength 6xx10^(-7) m is equal to :-
View SolutionIn a two slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the slits.If screen is moved by 5 xx 10^(-2) m towards the slits, then change in fringe width is 3 xx 10^(-5) m. If the distance between slits is 10^(-3) m, then wavelength of the light used will be :
View Solution3×10−7 मी की दूरी पर स्थित दो स्लिटों से समान कला में निकलते हुए 5000 Å तरंगदैर्ध्य वाले प्रकाश से यंग का द्वि-स्लिट प्रयोग किया जाता है। t=1.5×10−7 मी मोटाई की एक पारदर्शी शीट एक स्लिट पर रख दी जाती है। शीट के पदार्थ का अपवर्तनांक μ=1.17 है व्यतिकरण चित्र का केन्द्रीय उच्चिष्ठ अक्ष कहाँ दिखाई देगा? पर्दे के द्वि-स्लिट से D = 1.0 मी की दूरी पर रखा जाता है।
View SolutionIn a Young's double slit experiment the separation between slits is 2 xx 10^(-3)m whereas the distance of screen from the plane of slits is 2.5m. Light of wavelengths in the range 2000-8000 Å is allowed to fall on the slits. Find the wavelengths in the visible region that will be present on the screen at 10^(-3) m from the central maxima.
View SolutionIn YDSE, the two slits are separated by 0.1 mm and they are
0.5 m from the screen. The wavelength of light used is 5000 Å. Find the distance
between 7th maxima and 11 th mimima on the upper side of screen.
View Solution

