Length of a string of density ρ and Young's modulus Y under tension is increased by 1n times of its original length If the velocity of transverse and longitudinal vibration of the string is same, find the value of such velocity.
√Yρn
⎷Yρ12
√Yρ
⎷Yρn32
The correct Answer is:B
V1=√Yρ= velocity of longitudinal waves
V2=√TρS= velocity of transverse waves
V1V2=1ρ√Y.Y△ll=Yρ√△ll
(As TS=Y△ll)
But △ll=lnl=1n
V1V2=Yρn12
V2=Yρn12
V=
⎷Vρn12
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct
44 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
Which of the following statements are incorrect?
View SolutionStatement I: A tuning fork is considered as a source of an acoustic wave of a single frequency as marked on its body. Statement II: The tuning fork cannot produce any of its harmonics due to its special nature of construction.
View SolutionIn a car race sound signals emitted by two cars are detected by the detector on the straight track at the end point of the race. Frequency observer is 330 Hz and 360 Hz and the original frequency is 300 Hz of both cars. Race ends with the separation of 100 m between the cars. Assume both cars move with constant velocity and velocity of sound is 330ms. Find the time taken by wining car.
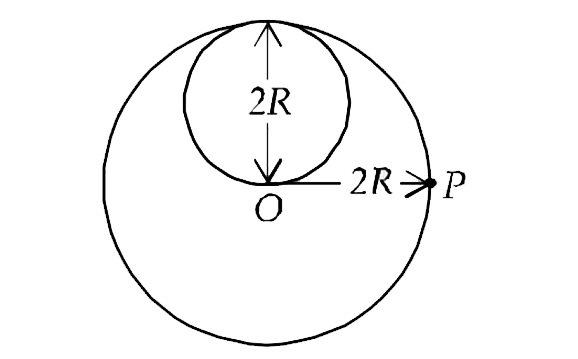
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO is
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionCalculate the velocity of a transverse wave along a string of length 2 m and mass 0.06 kg under a tension of 500 N .
View SolutionLength of a string of density ρ and Young's modulus Y under tension is increased by 1n times of its original length If the velocity of transverse and longitudinal vibration of the string is same, find the value of such velocity.
View SolutionA string is under tension so that its length is increased by 1/n times its original length . The ratio of fundamental frequency of longitudinal vibrations and transverse vibrations will be
View SolutionThe frequency of transverse vibrations in a stretched string is 200 Hz . If the tension is increased four times and the length is reduced to one-fourth the original value, the frequency of vibration will be
View SolutionA string is under tension sot that its length uncreased by 1/n times its original length . The ratio of fundamental frequency of longitudinal vibrations and transverse vibrations will be
View SolutionThe frequency of transverse vibration on a stretched string is 150 Hz. If the tension is increases four times and length is reduced to one fourth of its original value, the frequency of vibration will be
View SolutionThe elongation in a stretched strings is 1n times its original length. Prove that the ratio of transverse wave velocity and longitudinal wave velocity in the strings is 1√n.
View Solutionएक रस्सी तनाव के अंतर्गत है, इसकी लम्बाई में वृद्धि वास्तविक लम्बाई की 1n गुना होती है। अनुदैर्ध्य तरंग की मूल आवृत्ति तथा अनुप्रस्थ तरंग की मूल आवृत्ति में अनुपात है
View SolutionThe frequency of transverse vibrations in a stretched string is 200 Hz . If the tension is increased four times and the length is reduced to one-fourth the original value, the frequency of vibration will be
View SolutionThe fundamental frequency of vibration of a stretched string is 200Hz . Find the frequency of the vibration if the tension increases four times and length is reduced to one fourth the original values
View SolutionCalculate the velocity of a transverse wave along a string of length 2m and mass 0.06kg under a tension of 500N.
View Solution

