Obtain the expression of electric field at any point by continuous distribution of charge on a volume.Solution in Gujrati
Suppose a continuous charge distribution in space has a charge density ρ.
Choose any convenient origin O and let the position vector of any point in the charge distribution be →r.
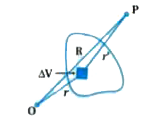
Divide the charge distribution into small volume elements of size ΔV.
The charge in a volume element ΔV is ρΔV.
Now, consider any general point P (inside or outside the distribution with position vector →R.
Electric field due to the charge ρΔV is given by Coulomb.s law.
→E=∑kρΔV(r.)2.ˆr
where r. is the distance between the charge element and P and f. is a unit vector in the direction from the charge element to P.
By the superposition principle, the total electric field,
→E=∫Vkρ.ΔV(r.)2ˆr=k≡ρΔVr2.ˆr
OR →E=k∫ρ.ΔVr−2.ˆr
In short, using Coulomb.s law and the superposition principle, electric field can be determined for any charge distribution, discrete or continuous or part discrete and part continuous.
Similar Questions
Obtain the expression of electric field by a plane of infinite size and with uniform charge distribution.
View SolutionObtain the expression of electric field by thir spherical shell with uniform charge distribution at a point outside it.
View SolutionObtain the expression of electric field by thin spherical shell with uniform charge distribution at a point inside it.
View SolutionObtain the expression of electric field by thir spherical shell with uniform charge distribution at a point outside it.
View SolutionObtain an expression for electric field intensity at any point on equitorial line of electric dipole. What is the direction of electric field?
View SolutionObtain an expression for electric field intensity at a point outside a charged conducting sphere.
View SolutionDistinguish between linear, surface and volume charge density. Obtain expression for force on a charge q due to continuous distribution of charge over a volume.
View Solution
