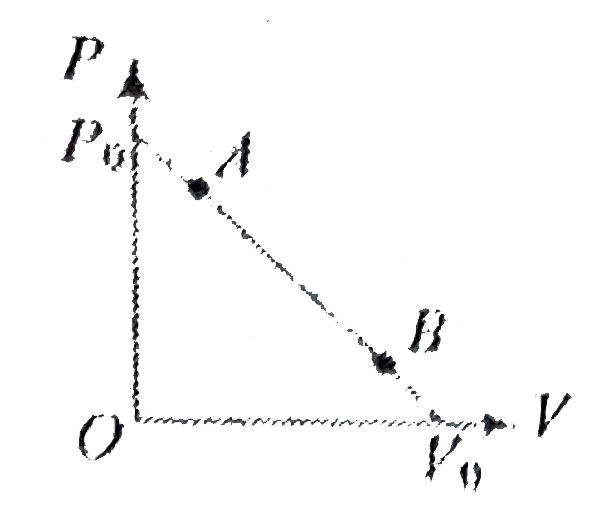
On an isothermal process ,there are two points A and B at which pressures and volumes are (2P0,V0) and (P0,2V0) respectively. A and B are connected by a straight line then , the temperature of the isothemal process is how much lower the maximum temperature :
P0V0nR
P0V02nR
3P0V02nR
P0V04nR
The correct Answer is:D
To solve the problem step by step, we will analyze the isothermal process between points A and B and calculate the temperature difference as required.
Step 1: Identify Given Values
We have two points A and B:
- Point A: Pressure PA=2P0, Volume VA=V0
- Point B: Pressure PB=P0, Volume VB=2V0
Step 2: Use the Ideal Gas Law
For an isothermal process, the temperature T can be calculated using the ideal gas equation:
PV=nRT
Thus, the temperature at point A can be expressed as:
TA=PAVAnR=(2P0)(V0)nR=2P0V0nR
Step 3: Calculate the Maximum Temperature
To find the maximum temperature, we need to determine the pressure and volume at the midpoint of the line connecting A and B.
1. Calculate the slope (m) of the line connecting points A and B:
m=PB−PAVB−VA=P0−2P02V0−V0=−P0V0=−P0V0
2. Equation of the line in the form P=mV+C:
- At point A: PA=2P0 and VA=V0
2P0=−P0V0⋅V0+C⟹C=3P0
Therefore, the equation of the line is:
P=−P0V0V+3P0
3. Substituting into the ideal gas law to find temperature:
T=PVnR=(−P0V0V+3P0)VnR
T=1nR(−P0V0V2+3P0V)
Step 4: Differentiate to Find Maximum Temperature
To find the maximum temperature, differentiate T with respect to V and set the derivative to zero:
dTdV=1nR(−P0V0⋅2V+3P0)=0
Solving for V:
−2P0V0V+3P0=0⟹V=3V02
Step 5: Calculate Maximum Temperature at V=3V02
Substituting V=3V02 back into the equation for P:
P=−P0V0⋅3V02+3P0=3P02
Now substituting P and V into the ideal gas equation:
Tmax=(3/2)P0(3/2)V0nR=9P0V04nR
Step 6: Calculate the Temperature Difference
Now we find the difference between the maximum temperature and the temperature at point A:
ΔT=Tmax−TA=9P0V04nR−2P0V0nR
Finding a common denominator:
ΔT=9P0V0−8P0V04nR=P0V04nR
Final Answer
The temperature of the isothermal process is P0V04nR lower than the maximum temperature.
---
We have two points A and B:
- Point A: Pressure PA=2P0, Volume VA=V0
- Point B: Pressure PB=P0, Volume VB=2V0
For an isothermal process, the temperature T can be calculated using the ideal gas equation:
PV=nRT
Thus, the temperature at point A can be expressed as:
TA=PAVAnR=(2P0)(V0)nR=2P0V0nR
To find the maximum temperature, we need to determine the pressure and volume at the midpoint of the line connecting A and B.
m=PB−PAVB−VA=P0−2P02V0−V0=−P0V0=−P0V0
- At point A: PA=2P0 and VA=V0
2P0=−P0V0⋅V0+C⟹C=3P0
Therefore, the equation of the line is:
P=−P0V0V+3P0
T=PVnR=(−P0V0V+3P0)VnR
T=1nR(−P0V0V2+3P0V)
To find the maximum temperature, differentiate T with respect to V and set the derivative to zero:
dTdV=1nR(−P0V0⋅2V+3P0)=0
Solving for V:
−2P0V0V+3P0=0⟹V=3V02
Substituting V=3V02 back into the equation for P:
P=−P0V0⋅3V02+3P0=3P02
Now substituting P and V into the ideal gas equation:
Tmax=(3/2)P0(3/2)V0nR=9P0V04nR
Now we find the difference between the maximum temperature and the temperature at point A:
ΔT=Tmax−TA=9P0V04nR−2P0V0nR
Finding a common denominator:
ΔT=9P0V0−8P0V04nR=P0V04nR
The temperature of the isothermal process is P0V04nR lower than the maximum temperature.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
For an ideal gas
View SolutionStatement I: A quasi -static process is so called bacause it is a sudden and large change of the system.
Statement II: An adiabatic process is not quasi- static because it is a sudden and large change of the system.
View SolutionFive grams of helium having rms speed of molecules 1000m/s and 24g of oxygen having rms speed of 1000m/s are introduced into a thermally isolated vessel. Find the rms speeds of helium and oxygen individually when thermal equilibrium is attained. Neglect the heat capacity of vessel.
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
The absolute temperature T versus volume V for the given process is
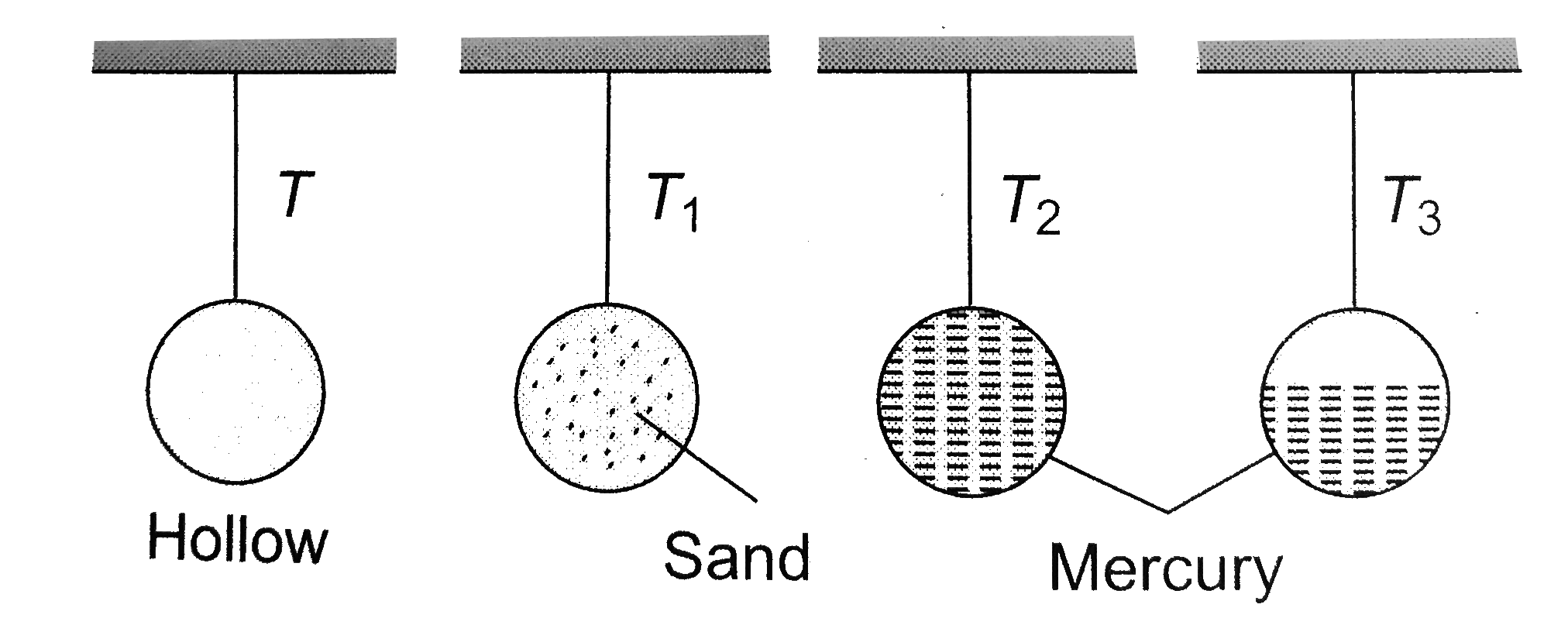
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
View SolutionTwo samples A and B are initaially kept in the same state. The sample A is expanded through an adiabatic process and the sample B through an isothermal process. The final volumes of the samples are the same . The final pressures in A and B are p_A and P_B respectively.
View SolutionFigure. Shows three processes for an ideal gas. The temperature at 'a' is 600 K, pressure of atm, and volume 1 L. The volume at 'b' is 4 L. Out of two processes, ab and ac, one is adiabatic and other is isothermal. The ratio of specific heats of the gas is 1.5. a. Which of the processes ab and ac is adiabatic ? Why b. Compute the pressure of the gas at b and c. c. Compute the temperature at b and c. d. Complete the volume at c.
View SolutionOn an isothermal process, there are two POINTs A and B at which pressures and volumes are (2P_(0), V_(0)) and (P_(0), 2V_(0)) respectively. If A and B are connected by a straight line, find the pressure at a POINT on this straight line at which temperature is maximum
View SolutionIn the previous problem, the temperature of the isothemal process is how much lower the maximum temperature :
View SolutionStatement-1: Two gases at same pressure, volume & temperature are compressed to same volume. The first isothermally and second adiabatically, greater work is done on the gas for an adiabatic process. Statement-2: Final temperature for gas going under isothermal process is more than gas going under adiabatic process.
View SolutionProcesses occur in leaves, which may lower their temperature is
View SolutionThe pressure and volume of a gas are P and V. If its pressure is reduced to P/2, by (A) isothermal process (B) by adiabatic process then the final volume will be :
View SolutionThe process in which changes in pressure, volume and temperature occur simultaneously is
View Solutionदो A तथा B पात्रों पर विचार कीजिए जिनमें समान दाब, आयतन तथा ताप पर आदर्श गैस भरी है। पात्र A की गैस को समतापीय प्रक्रम द्वारा उसके मूल आयतन के आधे आयतन तक संपीडित किया जाता है जबकि पात्र B की गैस को रुद्धोष्म प्रक्रम द्वारा उसके मूल आयतन के आधे आयतन तक संपीडित किया जाता है। B में गैस तथा A में गैस के अंतिम दाबों का अनुपात है
View SolutionIn Haber's process for NH3 the temperature and pressure are respectively
View Solution

