One end of V-tube containing mercury is connected to a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizental at an angle of 45∘ each. A small pressure difference is created between two columns when the suction pump is removed. Will the column of mercury in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Find the time period of oscillation.Solution in Gujrati
Figure shown as below

Let small liquid column of length dx is in the left of tube at x height from horizontal
Potential energy due to dx element,
d(PE)=dmgx [PE= from mgh ]
=pVgx [∴m=pV and V=Adx]
=pAdxgx
=pAgxdx
Total potential energy of liquid in left column
P.E=∫h10Apgxdx
=Apg∫h10xdx
=Apg[x22]h10=Apgh212
From figure h1=lsin45∘=l√2
∴P.E=Apgl24
Total potential energy of liquid in V-tube
P.E=Apgl24+Apgl24
Initial P.E.=Apgl24 .......(1)
When the suction pump is removed and due to pressure difference, let element moves towards right side by y unit.
Then the liquid column in left arm =(l−y)
And the liquid in right arm =l+y
Total potential energy =Apg(l−y)2sin245∘+Apg(l+y)2sin245∘
Final P.E.=Apg(l−y)22+Apg(l+y)22 ......(2)
Potential energy difference
△PE= final P.E. - initial P.E.
=Apg2[(l−y)2+(l+y)2−l2] [From equation (1) and (2) ]
=Apg2[2l2+2y2−l2]
=Apg2[l2+2y2] ........(3)
If change in velocity v of total liquid column
△KE=12mv2 [ where m=pV=pA×2l]
△KE=Aplv2 .......(4)
From law of conservation of energy,
△PE+△KE=0
Apg(l2+2y2)+Aplv2=0 .........(5)
Difference w.r.t time .t.
Apg[ddt(l2+2y2)]+Aplddt(v2)=0
Apg(0+2ydydt)+Apl(2vdvdt)=0
2Apgyv+Apl(2v)a=0
Dividing by 2Apv,
gy+la=0 [∴2Apv≠0]
∴a=−gly, comparing with this to
d2ydt2=−ω2y
∴ω=√gl
∴2πT=√gl
∴T=2π√lg is time period.
Topper's Solved these Questions
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
Explore 66 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)
Explore 20 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)
Explore 6 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Book:KUMAR PRAKASHANChapter:OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Exercise:CHAPTER - 8 (Match Type questions)
Explore 5 Videos
- PHYSICAL WORLDBook:KUMAR PRAKASHANChapter:PHYSICAL WORLDExercise:SECTION-E (QUESTIONS FROM MODULE)
Explore 9 Videos
Similar Questions
A particle executes SHM along X-axis. The force acting on it is given by……….
View SolutionA particle executes simple harmonic motion with an amplitude A. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude form the equilibrium position is………..
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
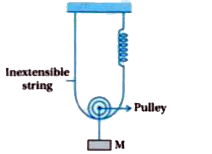 .
.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View SolutionOne end of V-tube containing mercury is connected to a suction grouup and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45^(@) each. A small pressure difference is created between two columns when the ssuction pump is removed. Will the column of mercuty in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Fing the time period of oscillation.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end is connected to the atmosphere. A small pressure difference is maintained between the two columns. Show that when the suction pump is removed, the liquid in the U-tube executes SHM.
View SolutionOne end of a V-tube containing mercury is connected ot a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45∘ each. A small pressure difference is created between two columns when the suction pump is removed. Will Neglect capillary and viscous forces. Find the time period of oscillation.
View Solutionपारे से भरी किसी U नली का एक सिरा किसी चूषण पंप से जुड़ा है, तथा दूसरा सिरा वायुमंडल में खुला छोड़ दिया गया है | दोनों स्तंभों में कुछ दाबांतर बनाए रखा जाता है | यह दर्शाइए कि जब चूषण पंप को हटा देते है, तब U नली में पारे का स्तंभ सरल आवर्त गति करता है |
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solutionपारे से भरी किसी U नली का एक सिरा किसी चूषण पंप से जुड़ा है , तथा दूसरा सिरा वायुमंडल में खुला छोड़ दिया गया है। दोनों स्तम्भों में कुछ दाबांतर बनाये रखा जाता है। यह दर्शाइए की जब चूषण पंप को हटा देते है , तब U - नली में पारे का स्तंभ सरल आवर्त गति करता है।
View Solutionपारे से भरी किसी U नली का एक सिरा किसी चूषण पंप से जुड़ा है, तथा दूसरा सिरा वायुमंडल में खुला छोड़ दिया गया है। दोनों स्तंभों में कुछ दाबान्तर बनाए रखा जाता है। यह दर्शाइए कि जब चूषण पंप को हटा देते हैं, तब U नली में पारे का स्तंभ सरल आवर्त गति करता है।
View SolutionOne end of U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solution
