Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
r=r1+r22
r=r1r2r1−r2
r=r1r2r1+r2
r=√r1r2
The correct Answer is:B
Step by step video, text & image solution for Prove that if two bubbles of radii r_(1) and r_(2)(r_(1)ltr_(2)) come in contact with each other then the radius of curvature of the common surface r=(r_(1)r_(2))/(r_(2)-r_(1)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A n object is weighed at the North Pole by a beam balance and a spring balance, giving reading of WB and WS respectively. It is again weighed in the same manner at the equator, giving readings of WB' and WS' respectively. Assume that the acceleration due to gravity is the same everywhere and that the balances are sensitive.
View SolutionIn the experimental setup for a photocell, the wavelength of the light incident on the cathod is initially 0.6 times the threshold wavelength for the material of the cathode. Certain change in the experimental setup are given in column A and their possibel effects are given in column B.
Column AColumn B(i)The intensity of the incident light is doubled but the frequency remains unaltered(a)Photocurrent remains the same(ii)Both the intensity and wavelength of the incident light are doubled(b)Photcurrent falls to zero(iii)The intensity of the incident light is doubled and its wavelength is made half(c)Stopping potential increase(iv)The intensity of the incident light ramains the same and the wavelength is made half(d)Photocurrent increases
View SolutionTwo waves travelling in a medium in the x-direction are represented by y1=Asin(αt−βx) and y2=Acos(βx+αt−π4), where y1 and y2 are the displacements of the particles of the medium t is time and α and β constants. The two have different :-
View SolutionIf r_(1),r_(2),r_(3) are the radii of the escribed circlesof a Delta ABC and ifr is the radius of its incircle then r_(1)r_(2)r_(3)-r(r_(1)R_(2)+r_(2)r_(3)+r_(3)r_(1))=
View SolutionProve that if two bubbles of radii r1 and r2 coalesce isothermally in vacuum then the radius of new bubble will be r=√r21+r22
View SolutionProve that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
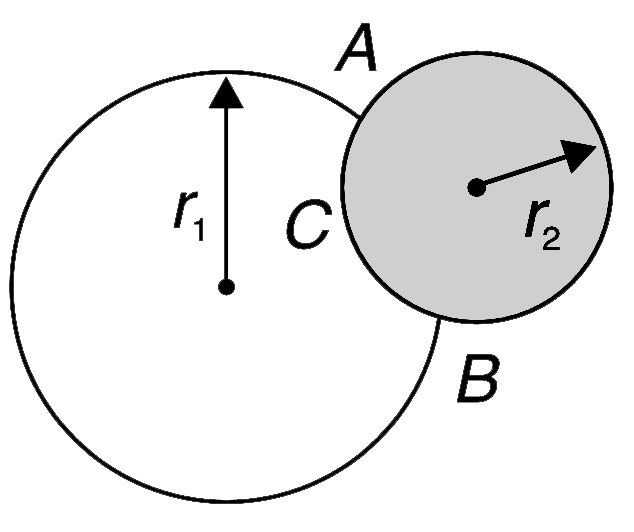
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionProve that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
View Solutionसाबुन के दो बुलबले जिनके त्रिज्याएँ r1 व r2(r1>r2) है , मिलकर एक हो जाते है । उनके उभयनिष्ठ पृष्ठ की त्रिज्या R होगी :
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View Solutionजब r1 व r2त्रिज्या वाले साबुन के दो बुलबुले मिलते है तो उभयनिष्ठ सतह की वक्रता त्रिज्या होती है (r2>r1) -
View SolutionIf r1,r3,r1 are the radii of the escribed circles of a ΔABC and if r is the radius of its incircle then r1r2r3−r(r1r2+r2r3+r3r1)=
View SolutionThe radii of two soap bubbles are r1andr2(r2<r1). They meet to produce a double bubble. The radius of their common interface is
View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View Solution

