[Q. Nos. 3-4] Difference in frequencies between 3rd overtone of closed pipe and 5th harmonic of the same pipe is 400 Hz. Further 3rd hormonic of this closed pipe is equal to 6th hormonic of another open pipe. If speed sound is 330 m/s. Then lengths of closed pipe and open pipe are a) 0.4125 m, 0.825 m b) 3.3m, 1.65 m c) 0.825 m, 0.825 m d) 1.65 m, 0.825 m
0.4125 m, 0.825 m
3.3m, 1.65 m
0.825 m, 0.825 m
1.65 m, 0.825 m
The correct Answer is:A
To solve the problem step by step, we will follow the information provided in the question and the video transcript.
Step 1: Understand the Frequencies of the Closed Pipe
The difference in frequencies between the 3rd overtone of a closed pipe and the 5th harmonic of the same pipe is given as 400 Hz.
- The frequency of the nth overtone (or harmonic) in a closed pipe is given by:
fn=(2n−1)v4L
where n is the harmonic number, v is the speed of sound, and L is the length of the pipe.
Step 2: Calculate the Frequencies
For the 3rd overtone (which is the 4th harmonic, n=4):
f4=(2⋅4−1)v4L=7v4L
For the 5th harmonic (n=5):
f5=(2⋅5−1)v4L=9v4L
Step 3: Set Up the Equation for Frequency Difference
The difference in frequencies is given as:
f4−f5=400 Hz
Substituting the expressions for f4 and f5:
7v4L−9v4L=400
This simplifies to:
−2v4L=400
−v2L=400
v=−800L
Step 4: Substitute the Speed of Sound
Given that the speed of sound v=330 m/s:
330=800L
Solving for L:
L=330800=0.4125 m
Step 5: Relate Closed and Open Pipe Frequencies
It is given that the 3rd harmonic of the closed pipe is equal to the 6th harmonic of another open pipe.
For the closed pipe (3rd harmonic):
f3=(2⋅3−1)v4L=5v4L
For the open pipe (6th harmonic):
f6=6v2Lo=3vLo
Setting these equal:
5v4L=3vLo
Step 6: Cancel v and Rearrange
Cancel v from both sides:
54L=3Lo
Cross-multiplying gives:
5Lo=12L
Substituting L=0.4125 m:
Lo=12⋅0.41255=0.825 m
Final Answer
The lengths of the closed pipe and the open pipe are:
- Length of closed pipe L=0.4125 m
- Length of open pipe Lo=0.825 m
Thus, the correct option is:
a) 0.4125 m, 0.825 m
The difference in frequencies between the 3rd overtone of a closed pipe and the 5th harmonic of the same pipe is given as 400 Hz.
fn=(2n−1)v4L
where n is the harmonic number, v is the speed of sound, and L is the length of the pipe.
For the 3rd overtone (which is the 4th harmonic, n=4):
f4=(2⋅4−1)v4L=7v4L
f5=(2⋅5−1)v4L=9v4L
The difference in frequencies is given as:
f4−f5=400 Hz
Substituting the expressions for f4 and f5:
7v4L−9v4L=400
This simplifies to:
−2v4L=400
−v2L=400
v=−800L
Given that the speed of sound v=330 m/s:
330=800L
Solving for L:
L=330800=0.4125 m
It is given that the 3rd harmonic of the closed pipe is equal to the 6th harmonic of another open pipe.
f3=(2⋅3−1)v4L=5v4L
f6=6v2Lo=3vLo
5v4L=3vLo
Cancel v from both sides:
54L=3Lo
Cross-multiplying gives:
5Lo=12L
Substituting L=0.4125 m:
Lo=12⋅0.41255=0.825 m
The lengths of the closed pipe and the open pipe are:
- Length of closed pipe L=0.4125 m
- Length of open pipe Lo=0.825 m
a) 0.4125 m, 0.825 m
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A sound source has frequency f. Source and observer both have same speed.For the apparent frequency observed by observer match the following.

View SolutionTwo wires of same material of radii 2r and r are welded together end to end The combination is used as a sonometer wire and is kept under tension T. The welded point lies midway between the bridges. What wil be the ratio of the number of loops formed in the wires, such that the joint is node when the stationary waves are set up in the wire?
View SolutionA stationary observer receiver a sound of frequency f0=2000Hz .Sourece is moving with constant velocity on a road at some non-zero prependicular distance from observer . The apparent frequncy f varies with times as show in figure . Speed of sound =300m/s. Find the maximum apparent frequency.
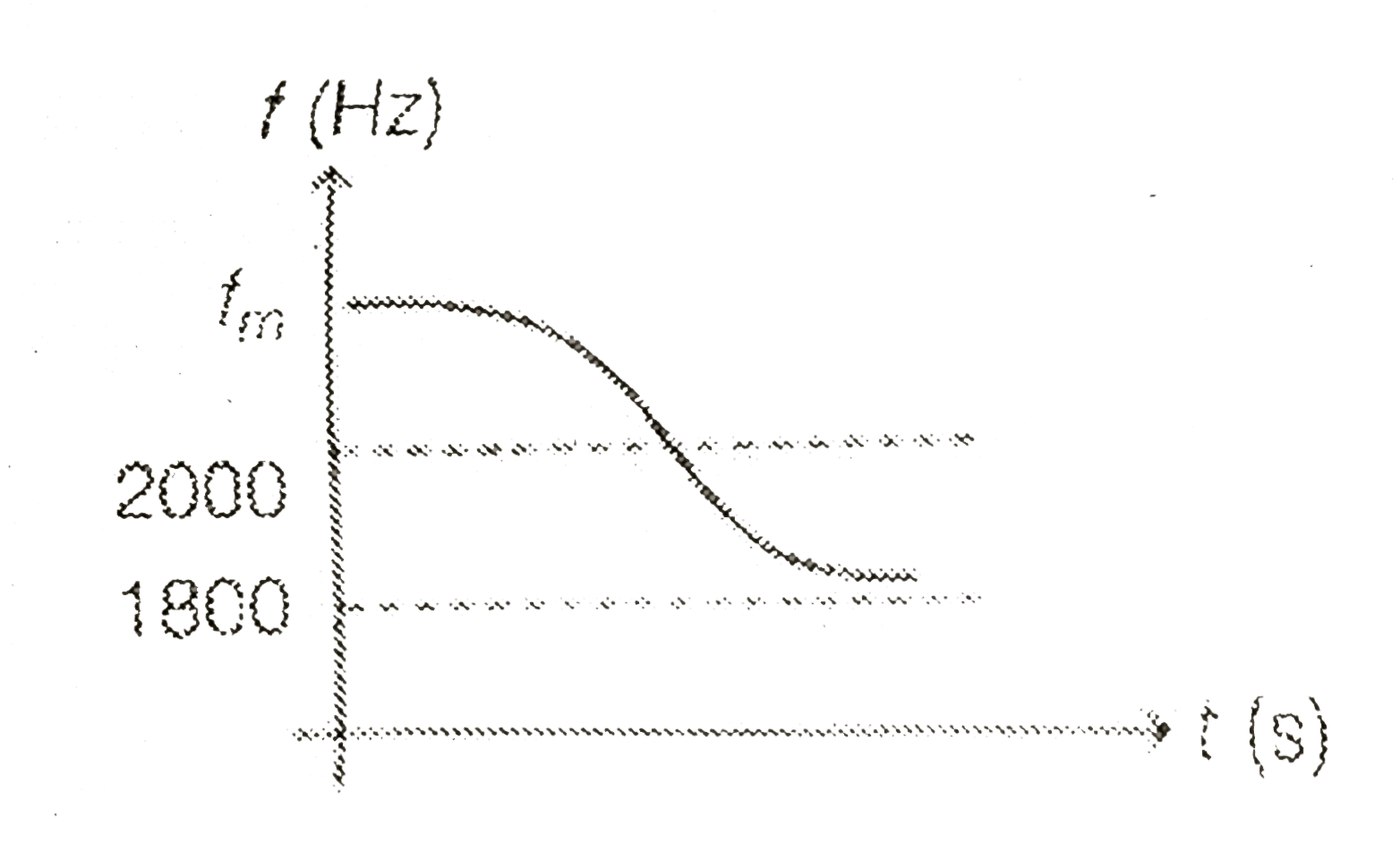
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vector, the angle between these Vector is
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
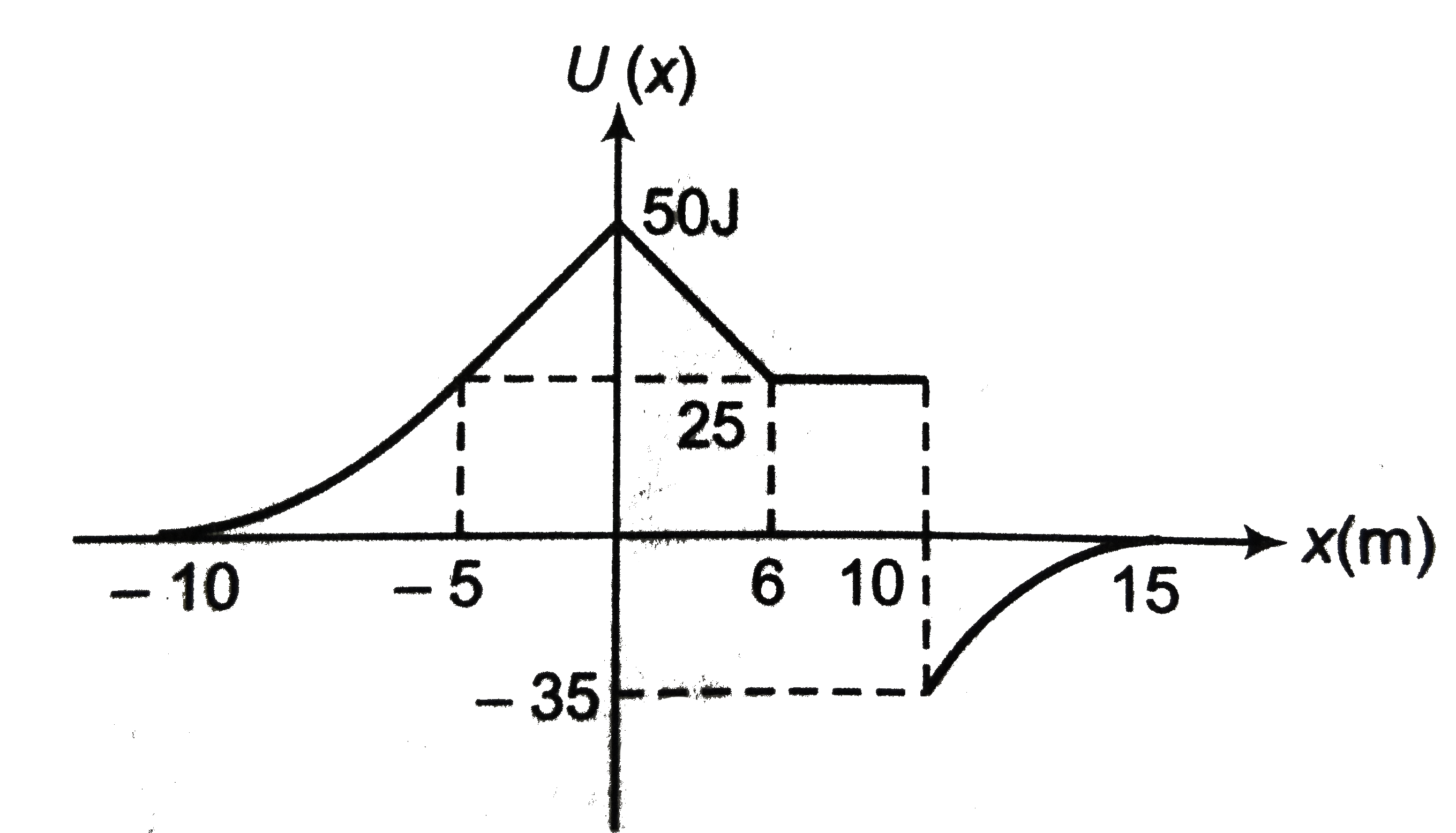
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionFundamental frequency of an open pipe of length 0.5 m is equal to the frequency of the first overtone of a closed pipe of length l . The value of l_(c) is (m)
View SolutionFirst overtone frequency of a closed organ pipe is equal to the first overtone frequency of an open organ pipe. Further nth harmonic of closed organ pipe is also equal to the nth harmonic of open pipe, where n and m are
View Solution[Q. Nos. 3-4] Difference in frequencies between 3rd overtone of closed pipe and 5th haronic of the same pipe is 400 Hz. Futher 3rd hormonic of this closed pipe os equal to 6th hormonic of another open pipe.
Fundamental frequencies of closed pipe and open pipe are
View Solution[Q. Nos. 3-4] Difference in frequencies between 3rd overtone of closed pipe and 5th haronic of the same pipe is 400 Hz. Futher 3rd hormonic of this closed pipe os equal to 6th hormonic of another open pipe.
If speed sound is 330 m/s. Then lengths of closed pipe and open pipe are
View Solutionकिसी खुले ऑर्गन पाइप की मूल आवृत्ति 300 हर्ट्स है। इस ऑर्गन पाइप का प्रथम अधिस्वरक उतना ही है जितना कि एक बन्द ऑर्गन पाइप का प्रथम अधिस्वरक। यदि ध्वनि की चाल 330 मीटर/सेकंड है, तो बन्द ऑर्गन पाइप की लम्बाई लगभग है:
View Solutionएक खुले ऑर्गन पाइप की मूल आवृत्ति 300 Hz है। एक दूसरे बन्द ऑर्गन पाइप के प्रथम अधिस्वरक की आवृत्ति वही है जो खुले पाइप के प्रथम अधिस्वरक की है। प्रत्येक पाइप की लम्बाई क्या है? ध्वनि की चाल 330 मीटर/सेकंड है।
View Solutionएक बन्द पाइप तथा एक खुला पाइप एक साथ 5 विस्पंद/सेकण्ड की ध्वनि उत्पन्न करते हैं । यदि खुले पाइप की लम्बाई सेमी है तो ज्ञात कीजिये कि बन्द पाइप की लम्बाई में क्या परिवर्तन करना होगा कि दोनों पाइप स्वरमेल में हों (ध्वनि कि चाल = 330 मीटर/सेकण्ड)
View SolutionIf speed of sound is 330 m/s. The lengths of closed pipe and open pipe are :
View SolutionFirst overtone frequency of a closed organ pipe is equal to the first overtone frequency of an open organ pipe. Further nth harmonic of closed organ pipe is also equal to the nth harmonic of open pipe, where n and m are:
View SolutionThe second overtone of an open pipe has the same frequency as the first overtone of a closed pipe 2 m long. The length of the open pipe is
View Solution

