Show that the oscillations due to a spring are simple harmonic oscillations and obtain the expression of periodic time.Solution in Gujrati
According to figure a block of mass m fixed to a spring, which in turn is fixed to a rigid wall.
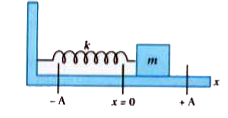
The block is placed on a friction less horizontal surface.
If the block is pulled on one side and is released it then executs a to and fro motion about a mean position.
Let x=0, indicate the position of the centre of the block when the spring is in equilibrium.
the positions -A and +A indicate the maximum displacement to the left and the right of the mean position.
For spring Robert Hooke law, ..Spring when deformed, is subject to a restoring force, the magnitude of which is proportional to the deformation or the displacement and acts is opposite direction...
Let any time t, if the displacement of the block form its mean position is x, the restoring force F acting on the block it
F(x)=−kx ............(1)
Where k is constant of proportionality and is called the spring constant or spring force constant.
Equation (1) is same as the force law for SHM and therefore the system executes a simple hormonic motion.
But F(x)=ma(x)
∴ma(x)=kx
∴m(−ω2x)=−kx [∴a(x)=−ω2x]
∴ω=√km
∴2πT=√km
∴T=2π√km
is the period of block attached with spring having small oscillations
∴T∝1√k (for a given block) and T∝√m (for a given spring) and frequency v=1T=12π√mk
Stiff spring have high value of k and period is small and frequency of oscillation is large. So the oscillation becomes rapid and for soft spring k is small and hence period is large and frequency of oscillation is small so oscillation becomes slowly.
Similar Questions
Show that for small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression for its time period. Does it depend on the mass of the bob ?
View SolutionIs oscillation of a mass suspended by a spring is simple harmonic?
View SolutionA loaded vertical spring executes simple harmonic oscillations with period of 4 s. The difference between the kinetic energy and potential energy of this system oscillates with a period of
View SolutionAs shown in figure, a simple harmonic motion oscillator having identical four springs has time period
View Solution(a) Define simple harmonic motion and derive, an expression for the period of simple harmonic motion by reference circle method.
(b) Derive an expression for the period of oscillations of a simple pendulum.
View SolutionTwo springs are made to oscillate simple harmonically due to the same mass individually. The time periods obtained are T1 and T2. If both the springs are connected in series and then made to oscillate by the same mass, the resulting time period will be
View SolutionA loaded vertical spring executes simple harmonic oscillations with period of 4 s. The difference between the kinetic energy and potential energy of this system oscillates with a period of
View SolutionIs oscillation of a mass suspended by a spring simple harmonic ?
View Solution
