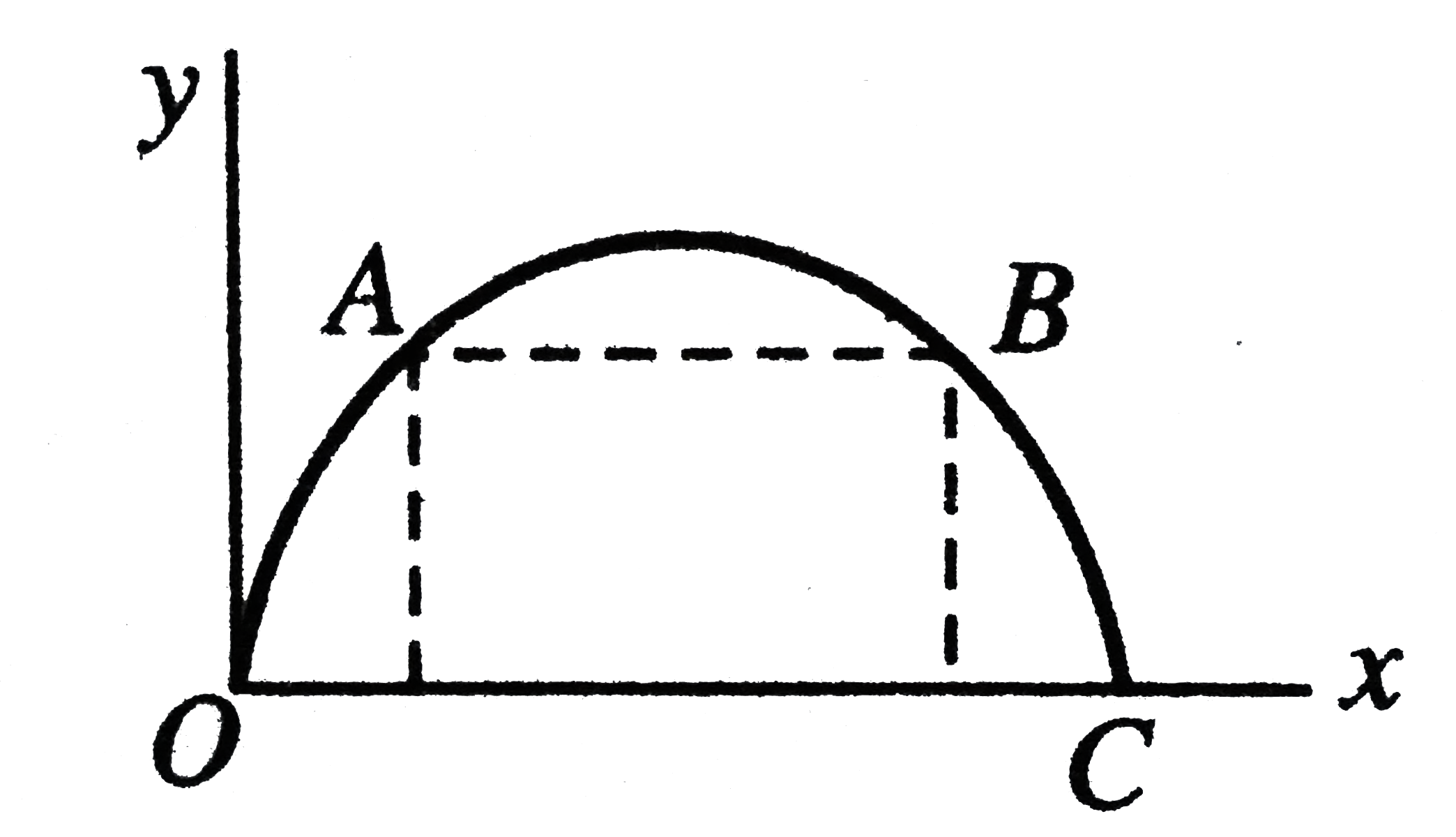
Show that there are two values of time for which a projectile is at the same height. Also show mathematically that the sum of these two times is equal to the time of flight.
A. 3T/2
B. 4T/3
C. 3T/4
D. T
The correct Answer is:D
(d) tOA=tBC
To find tOA+tOB,
tOA+tOB=tBC+(tOB)=T.
 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 39 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionThe projectile has only vertical component of velocity at the highest point of its trajectory.
At the highest point, only one component of velocity is present.
View SolutionTwo particles were projected one by one with the same initial velocity from the same point on level ground. They follow the same parabolic trajectory and are found to be in the same horizontal level, separated by a distance of 1m,2s after the second partice was projected. Assume that the horizontal component of their velocities is 0.5ms−1. Find
(a) the horizontal range of the parabolic path.
(b) the maximum height for the parabolic path.
View SolutionA man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v with respect to himself and catches it after t1 seconds. After wards when the lift is descending with the same acceleration a acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after t2 seconds?
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
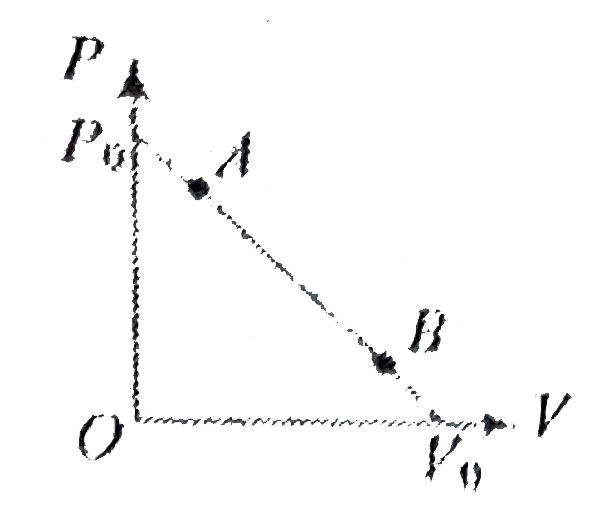
The absolute temperature T versus volume V for the given process is
View SolutionTIME OF FLIGHT, MAXIMUM HEIGHT AND RANGE OF PROJECTILE MOTION
View SolutionShow that there are two values of time for which a projectile is at the same height. Also show mathematically that the sum of these two times is equal to the time of flight.
View SolutionAssertion : If time of flight in a projectile motion is made two times, its maximum height will become four times. Reason : In projectile motion H prop T^2 , where H is maximum height and T the time of flight.
View SolutionA projectile can have same range R for two angles of projection. It t_1 and t_2 are the times of flight in the two cases, then what is the product of two times of flight ?
View SolutionShow that there are two values of time for which is projectile is at the same height. Also show that the sum of these two times is equal to the time of flight.
View SolutionThere are two values of time for which a projectile is at the same height. The sum of these two times is equal to (T = time of flight of the projectile)
View SolutionShow that the horizontal range of a projectile is same for two angles of projection . Is the sum of maximum heights for these two angles dependent on the angle of projectile ?
View SolutionTwo projectiles are projected from the same point different velocities and different angles of projection .If the maximum height attained by both the projectiles is same, show that sum of the times taken by each to reach the highest point is equal to the total time of flight of either of the projectiles .
View SolutionA projectile has same range R for the two angles of projection. If T_(1) and T_(2) are the times of flight in two cases, then:
View SolutionShow that a projectile fired at an angle 0 with the horizontal crosses a certain height at two timings t_(1) and t_(2) and the sum of these two is equal to :
View SolutionTwo projectiles are thrown with different velocities and at different angles so as to cover the same maximum height. Show that the sum of the times taken by each to reach the highest point is equal to the total time taken by either of the projectiles.
View Solution
