Sphere A of mass 'm' moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres vA:vB after collision will be :
1−e1+e
1+e1−e
e+1)e−1
e−1e+1
The correct Answer is:B
From conservation of linear momentum:
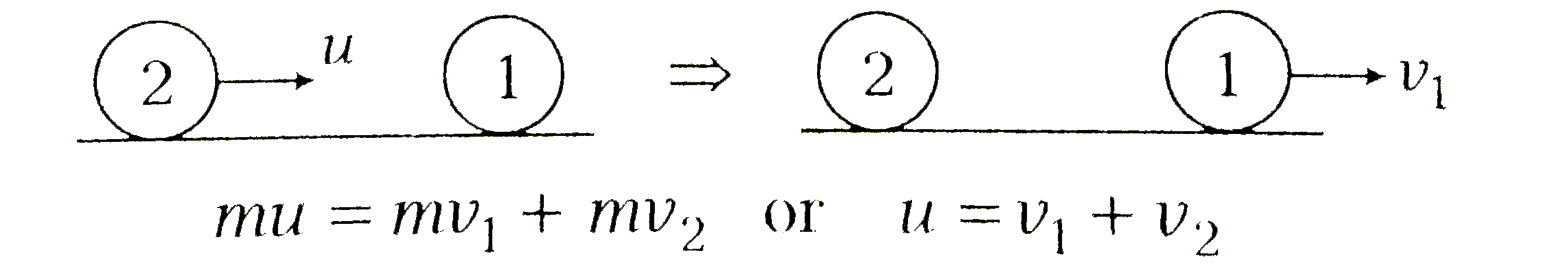
From definition of e,
v1−v2=eu..............(ii)
Solving these two equations, we get
v1=1+e2u and v2=1−e2u
∴ ⎛⎜⎝v1v2=1+e1−e
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A bullet of mass a and velocity b is fired into a large block of mass c. The final velocity of the system is
View SolutionThese questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following five responses.
Reason: For inelastic collision, 0≤e<1. Hence, the magnitude of relative velocity of separation after collision is less than relative velocity of approach before collision.
View SolutionA rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......
View SolutionA black body is at a temperature of 5760K. The energy of radiation emitted by the body at wavelength 250nm is U1 at wavelength 500nm is U2 and that at 1000nm is U3. Wien's consant, b=2.88×106nmK. Which of the following is correct?
View SolutionComprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction), we can apply: ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is velocity and a the acceleration (all with respect to ground).
A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is ..........m/s :-
View SolutionA sphere A of mass m moving with a velocity hits another stationary sphere B of same mass. If the ratio of the velocity of the sphere after collision is (v_(A))/(v_(B)) = (1 - e)/(1 + e) where e is the cofficient of restitution, what is the initial velocity of sphere A with which it strikes?
View SolutionA sphere of mass m moving with constant velocity u , collides with another stationary sphere of same mass. If e is the coefficient of restitution, the ratio of the final velocities of the first and second sphere is
View SolutionSphere A of mass 'm' moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres vA:vB after collision will be :
View SolutionA sphere of mass 'm' moving with velocity 'v' collides head-on on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is (e is coefficient of restitution and collision is inelastic)
View SolutionA sphere of mass m moving with a constant velocity hits another stationary sphere of the same mass, if e is the coefficient of restitution, then ratio of speed of the first sphere to the speed of the second sphere after collision will be
View SolutionA sphere of mass m moving with a constant velocity V hits another sphere of equal mass at rest. If e is the coefficient of restitution, then the ratio of velocities former to latter of the two spheres after collision will be:
View SolutionA sphere of mass m moving with a velocity u hits another sphere of same mass at rest. If e is the coefficient of restitution then the ratio of velocities of two spheres after collision will be :
View SolutionA sphere of mass m moving with a uniform velocity v hits another identical sphere at rest. If the coefficient of restitution is e, the ratio of the velocities of the two sphere after the collision is (e-1)/(e+1) .
View Solutionm द्रव्यमान का एक गोला नियत वेग से गतिशील है तथा समान द्रव्यमान के अन्य स्थिर गोले पर टकराता है। यदि e प्रत्यास्थता गुणांक है, तब संघट्ट के बाद गोले के वेग का अनुपात होगा
View SolutionA sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass and of coefficient of restitution (e). The ratio of velocities of the two spheres, after collision, will be
View SolutionA sphere of mass 'm' moving with velocity 'v' collides head-on on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is (e is coefficient of restitution and collision is inelastic)
View Solution

