Sppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are
![Sppose that a point mass 'm' is moving under a constant force vecF = 2hati-hatj + hatk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e., tau= vecr xx vecF . At P, torque can be expessed as tau= (-4hatj - 4 hatk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x(1), y(1), z(1)) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force vecF as its adjacent sides , area of this parallelogram is 2sqrt(2)m^(2) . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are Answer the following questions. Coordinates of P are :](https://d10lpgp6xz60nq.cloudfront.net/physics_images/GRB_AM_PHY_C03_E01_174_Q01.png)
Answer the following questions.
Coordinates of P are :
The correct Answer is:C
τp=→rpo×→F
=(xi+yj−ˆk)×(2i−j+ˆk)
→τp=(y−1)i−(x+2)j−(x+2y)ˆk
Given →τp=−4ˆj−4ˆk
∴ x=2andy=1
Also, →rPQ=(x1−x)i+(y1−y)j+(z1+1)ˆk
Given →rPQ⊥→F
∴ →rPQ.→F=0
∴[(x1−2)ˆi+(y1−1)ˆj+(z1+1)ˆk].[2i−ˆj+ˆk]=0......(i)
τQ=→rQO×→F=∣∣
∣
∣∣ijkx1y1z12−11∣∣
∣
∣∣
τQ=(y1+z1)ˆi−j(x1−2z1)+k(−x1−2y1)
Given, y1+z1=0 ...........(ii)
And, x1−2z1=x1+2y1 ......(iii)
Also, ∣∣→rQO×→F=10√2
∴(y1+z1)2+(x1−2z1)2+(x1+2y1)2=100×2....(iv)
∴ 2(x1−2z1)2=100×2
∴ x1−2z1=10
∴ →τQ=−10ˆj−10ˆk
W=0, as →rPQ is prependicular to →F
Topper's Solved these Questions
Similar Questions
Consider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
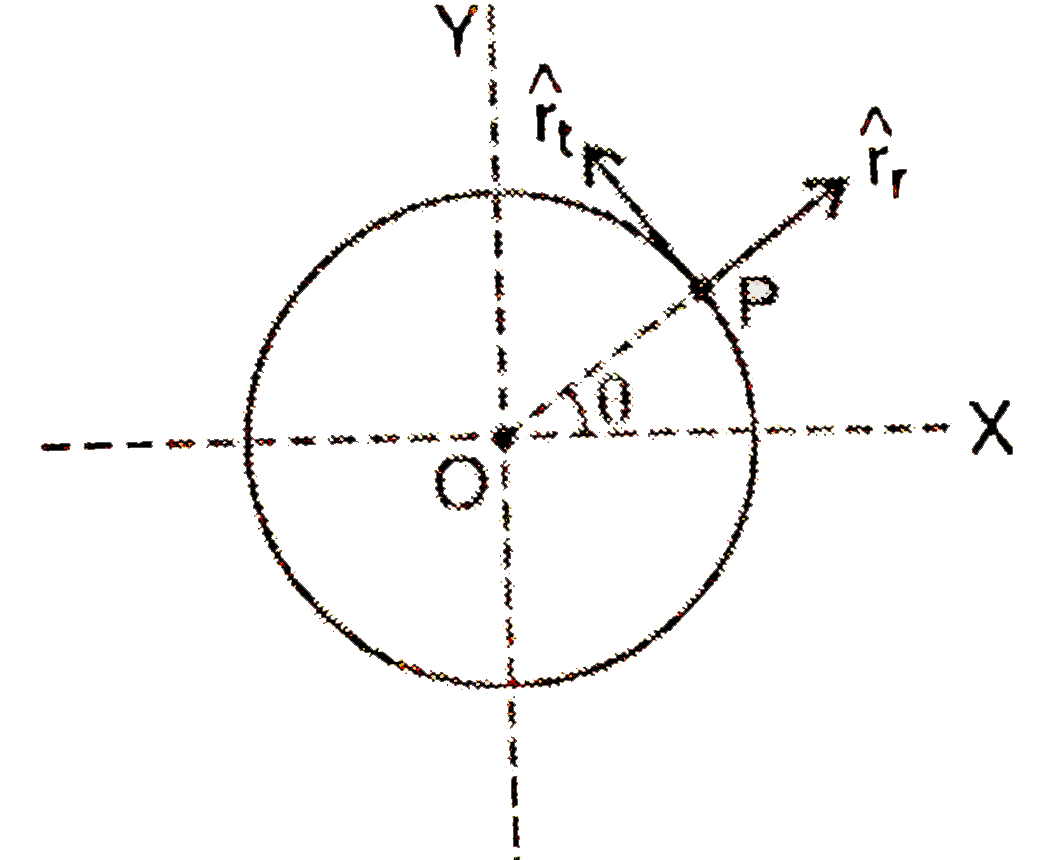
Answer the following questions :
For any instantantaneous position of the objected P, the radial unit vector ˆrr can be expressed as :
View SolutionIf force, mass and time are taken to be base physical quantities with dimensional formula [F], [M] and [T], then :
Dimensional formula for energy is :
View SolutionThe torque of a force vecF=-3hati+hatj+5hatk acting at a point is vectau . If the position vector of the point vector of the point is 7hati+3hatj+hatk , then vectau is :
View SolutionA constant force →F=2ˆi−ˆj−ˆk moves a particle from position vector
→r1=−5ˆi−4ˆj+ˆk to position vector →r2=−7ˆi−2ˆj+2ˆk . What will be the work done by this force ?
View Solutionबल F=−3ˆi+ˆj+5ˆk का बलाघूर्ण किसी बिन्दु र पर आरोपित है। यदि उस बिन्दु का स्थिति सदिश 7ˆi+3ˆj+ˆk है, तब τ है
View SolutionIf a position vector of a point is →r=7ˆi+3ˆj+ˆk and force acting on it is →F=−3ˆi+ˆj+5ˆk then find torque.
View SolutionThe work done in moving an object from origin to a point whose position vector is →r=3ˆi+2ˆj−5ˆk by a force →F=2ˆi−ˆj−ˆk is
View SolutionThe work done in moving an object from origion to a point whose position vector is →r=3ˆi+2ˆj−5ˆk by a force →F=2ˆi−ˆj−ˆk is
View Solution

