Statement I: The specific heat of a gas in an adiabatic process is zwero but it is infinite in an isothermal process.
Statement II: Specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in termperature.
Statement I: is true, Statement II is true and Statement II is the correct explanation for Statement I.
Statement I: is true, Statement II is true and Statement II is NOT the correct explanation for Statement I.
Statement I is true, Statement II is false.
Statement I is false, Statement II is true.
The correct Answer is:C
To solve the question, we need to analyze both statements provided and determine their validity.
Step 1: Analyze Statement I
Statement I claims that the specific heat of a gas in an adiabatic process is zero, while in an isothermal process, it is infinite.
- Adiabatic Process: In an adiabatic process, there is no heat exchange with the surroundings (dq = 0). The specific heat (C) is defined as:
C=dqdT
Since dq = 0, it follows that:
C=0dT=0
Therefore, the specific heat in an adiabatic process is indeed zero.
- Isothermal Process: In an isothermal process, the temperature remains constant (dT = 0). The specific heat is again defined as:
C=dqdT
Since dT = 0, it follows that:
C=dq0=∞
Therefore, the specific heat in an isothermal process is infinite.
Conclusion for Statement I: True.
Step 2: Analyze Statement II
Statement II states that the specific heat of a gas is directly proportional to the heat exchanged with the system and inversely proportional to the change in temperature.
- The specific heat (C) is defined as:
C=dqdT
This means that specific heat is the amount of heat (dq) required to raise the temperature (dT) of a unit mass of the substance by one degree.
- The statement claims that specific heat is directly proportional to dq and inversely proportional to dT. This is misleading because while it is true that:
C∝dqandC∝1dT
it does not imply a direct relationship in the form of a simple proportionality constant. The specific heat is defined through the ratio of these two quantities, not as a direct proportionality.
Conclusion for Statement II: False.
Final Conclusion
- Statement I is true.
- Statement II is false.
Statement I claims that the specific heat of a gas in an adiabatic process is zero, while in an isothermal process, it is infinite.
C=dqdT
Since dq = 0, it follows that:
C=0dT=0
Therefore, the specific heat in an adiabatic process is indeed zero.
C=dqdT
Since dT = 0, it follows that:
C=dq0=∞
Therefore, the specific heat in an isothermal process is infinite.
Statement II states that the specific heat of a gas is directly proportional to the heat exchanged with the system and inversely proportional to the change in temperature.
C=dqdT
This means that specific heat is the amount of heat (dq) required to raise the temperature (dT) of a unit mass of the substance by one degree.
C∝dqandC∝1dT
it does not imply a direct relationship in the form of a simple proportionality constant. The specific heat is defined through the ratio of these two quantities, not as a direct proportionality.
- Statement I is true.
- Statement II is false.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Comprehension
56 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
28 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
A fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find pressure at C
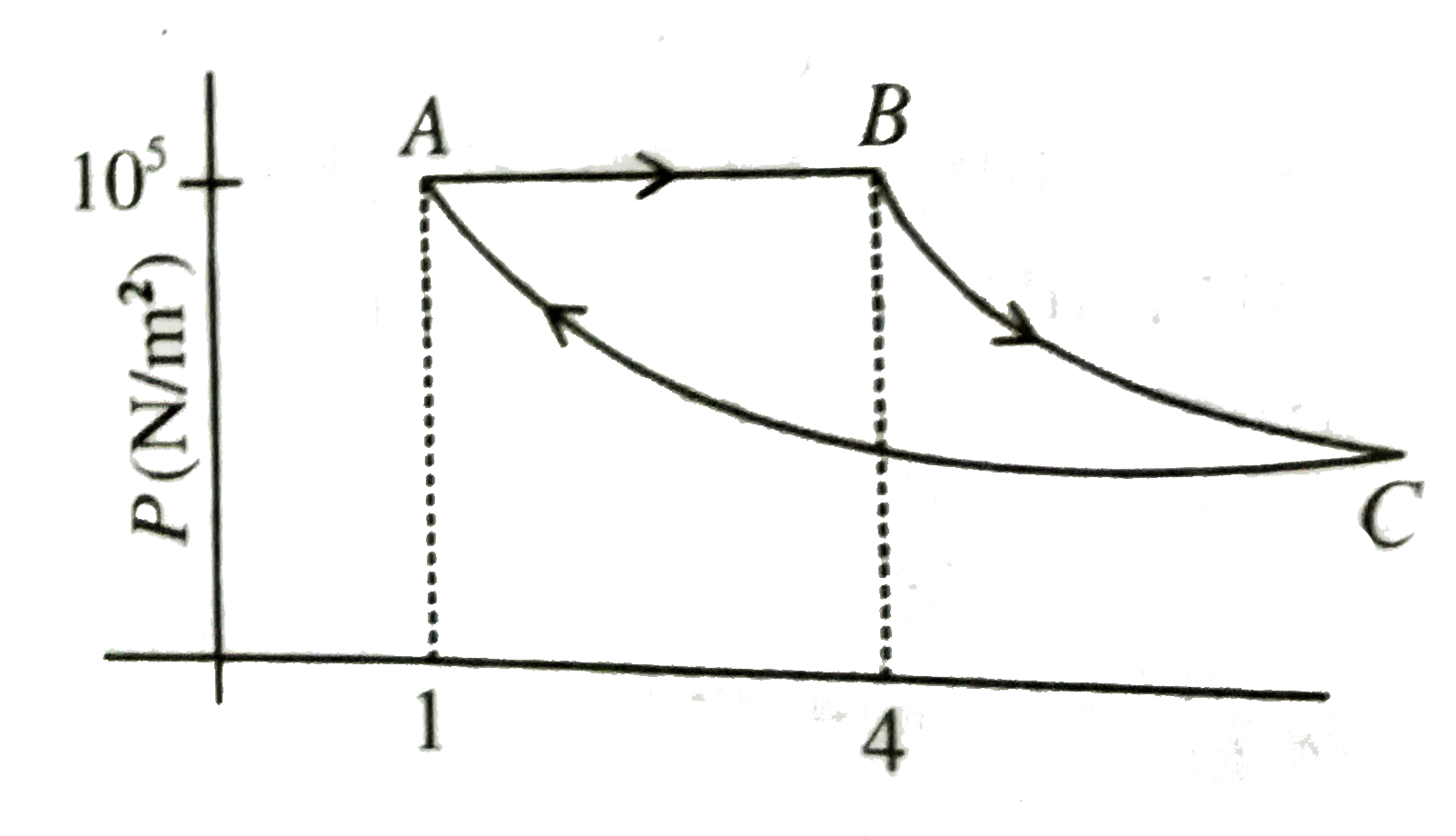
.
View Solution8g of oxygen, 14 g of nitrogen and 22 g carbon dioxide are mixed in an encloser of volume 10 litre and temperature 27∘C. Calculate the pressure exerted by the mixture , R=8.3Jmole−1K−1, Molecular weight of oxygen , nitrogen and carbon 32 , 28 and 44 respectively.
View SolutionFor an ideal gas
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
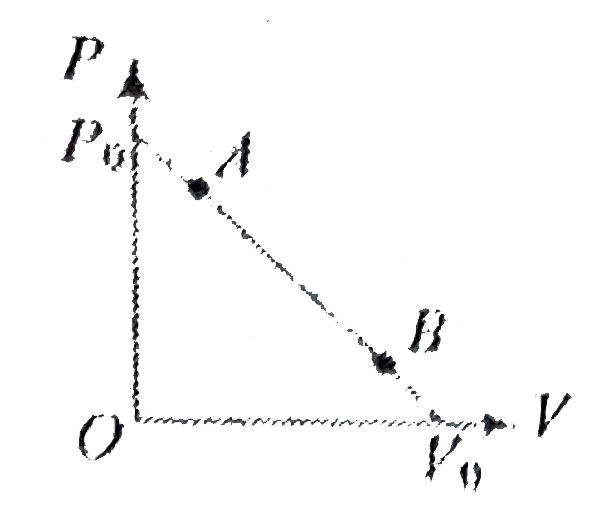
The absolute temperature T versus volume V for the given process is
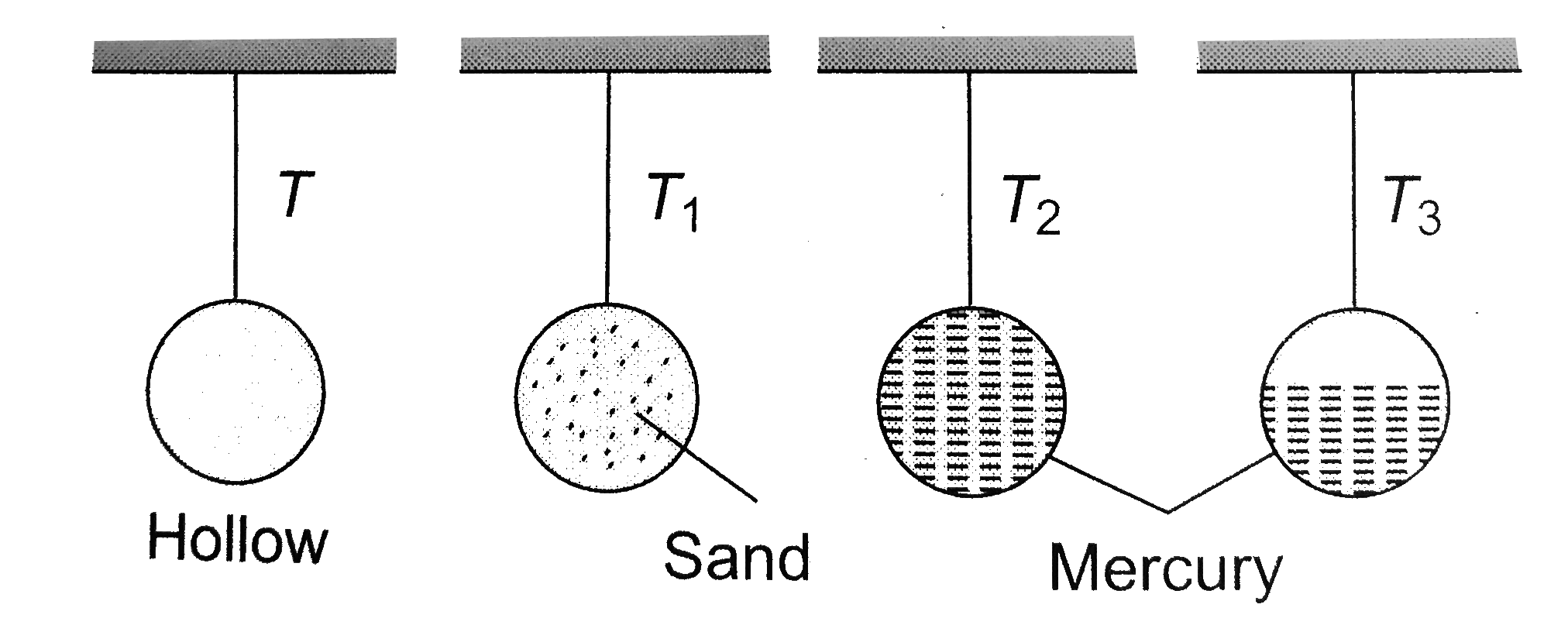
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
View SolutionStatement I: The specific heat of a gas in an adiabatic process is zwero but it is infinite in an isothermal process. Statement II: Specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in termperature.
View SolutionWhat is specific heat of a gas is an isothermal process?
View SolutionWhat is specific heat of a gas is an adiabatic process?
View SolutionThe specific heat of a gas in an isothermal process is
View SolutionWhat is specific heat of a gas in an isothermal process ?
View SolutionWhat is the specific heat of a gas in an adiabatic process ?
View SolutionWhat are the values of specific heat of a gas in isothermal and adiabatic processes?
View SolutionA : The specific heat of an ideal gas is zero in an adiabatic process. R : Specific heat of a gas is process independent.
View SolutionStatement I : The specific heat of a gas in an adiabatic process is zero but it is infinite in an isothermal process. Statement II : Molar specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in temperature.
View Solutionप्रक्कथन :रुद्धोम प्रक्रिया में किसी गैस की विशिष्ट ऊष्मा शून्य एवं समतापीय प्रक्रिया में अनन्त होती है।
कारण :किसी गैस की विशिष्ट ऊष्मा निकाय के ऊष्मा परिवर्तन के अनुक्रमानुपाती एवं ताप परिवर्तन के व्युत्क्रमानुपाती होती है।
View Solution

