The coordinates of a particle moving in a plane are given by x=acospt and y=bsinpt where a,b(<a) and p are positive constants of appropriate dimensions. Then,
The path of the particle is an ellipse.
The velocity and acceleration of the particle are normal to each other at t=π/2p.
The acceleration of the particle is always directed towards a focus.
The distance travelled by the particles in time interval t=0→t=π/2p is a.
The correct Answer is:A, B
a,b. x=acos(pt),y=bsin(pt)
Equation of path in x-y plane is
[xa]2+[yb]2=1
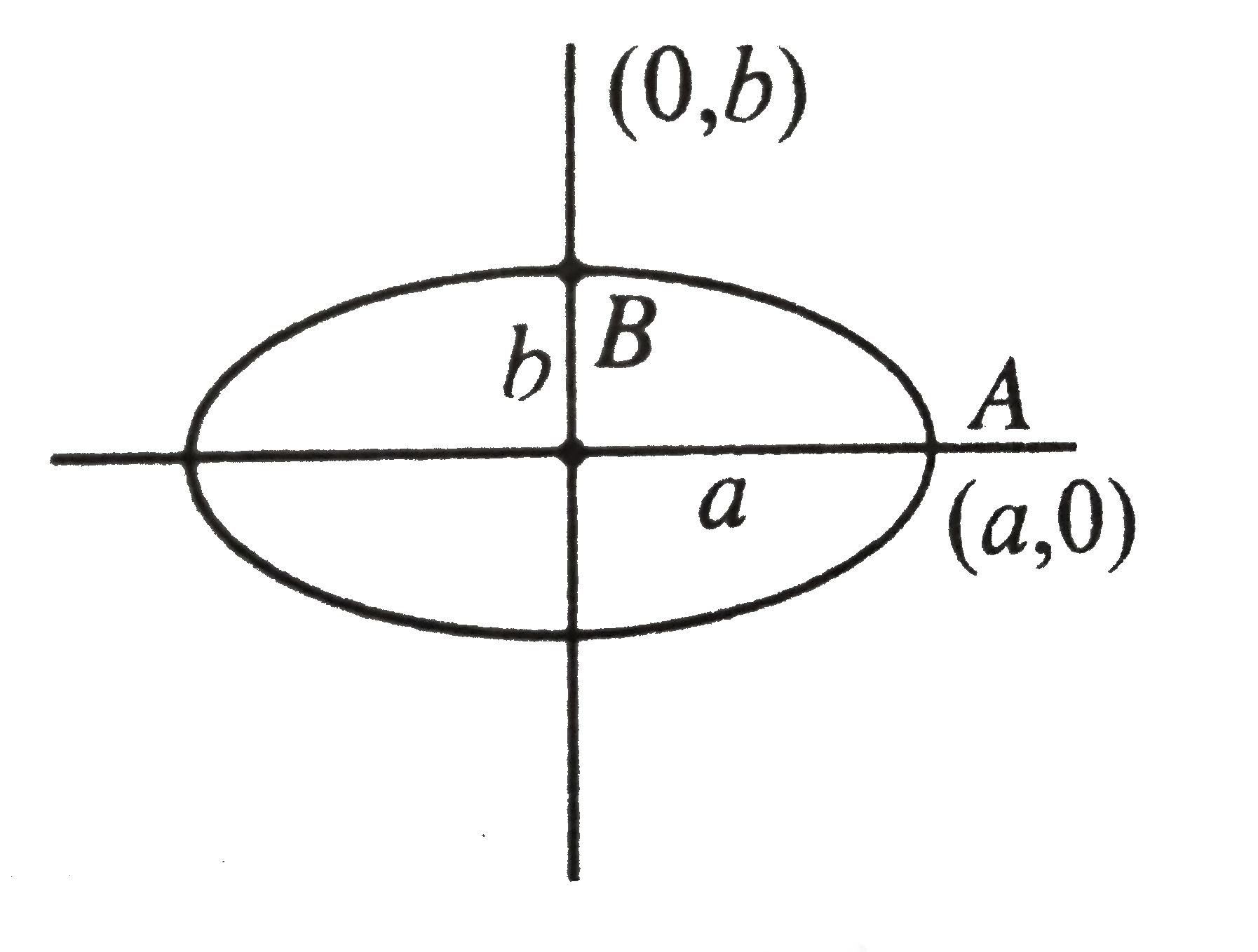
i.e., the path of the particle is an ellipse.
Position vector of a point P is
→r=acosptˆi+bsinptˆj
⇒→v=p(−asinptˆi+bcosptˆj)
and →a=−p2(−acosptˆi+bsinptˆj)=−p2→r
Acceleration of directed towards the centre.
Also , →v⋅→a=0att=π/2p
At t=0,→r=aˆi
At t=π/2p,→r=bˆj
So in time t=0→t=π/2p, particle goes from A to B travelling
a distance more than a.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Linked Comprehension Type
Explore 35 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Integer Type
Explore 17 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
The coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionThe coordinates of a particle moving in XY-plane vary with time as x=4t2,y=2t. The locus of the particle is a : -
View SolutionThe coordinates of a moving particle at any time t are given by x=ct and y=bt2. The speed of the particle is given by
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionThe coordinates of a particle moving in XY-plane very with time as x=4t2,y=2t. The locus of the particle is
View SolutionA particle moves in xy plane accordin to the law x=asinwt and y=a(1−coswt) where a and w are costant . The particle traces.
View SolutionThe potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
View SolutionThe position co-ordinates of a particle moving in a 3-D coordinate system is given
by x=a coswt
y=a sinwt
and z=awt
The speed of the particle is :
View SolutionThe position co-ordinates of a particle moving in a 3-D coordinate system is given
by x=a coswt
y=a sinwt
and z=awt
The speed of the particle is :
View Solution
