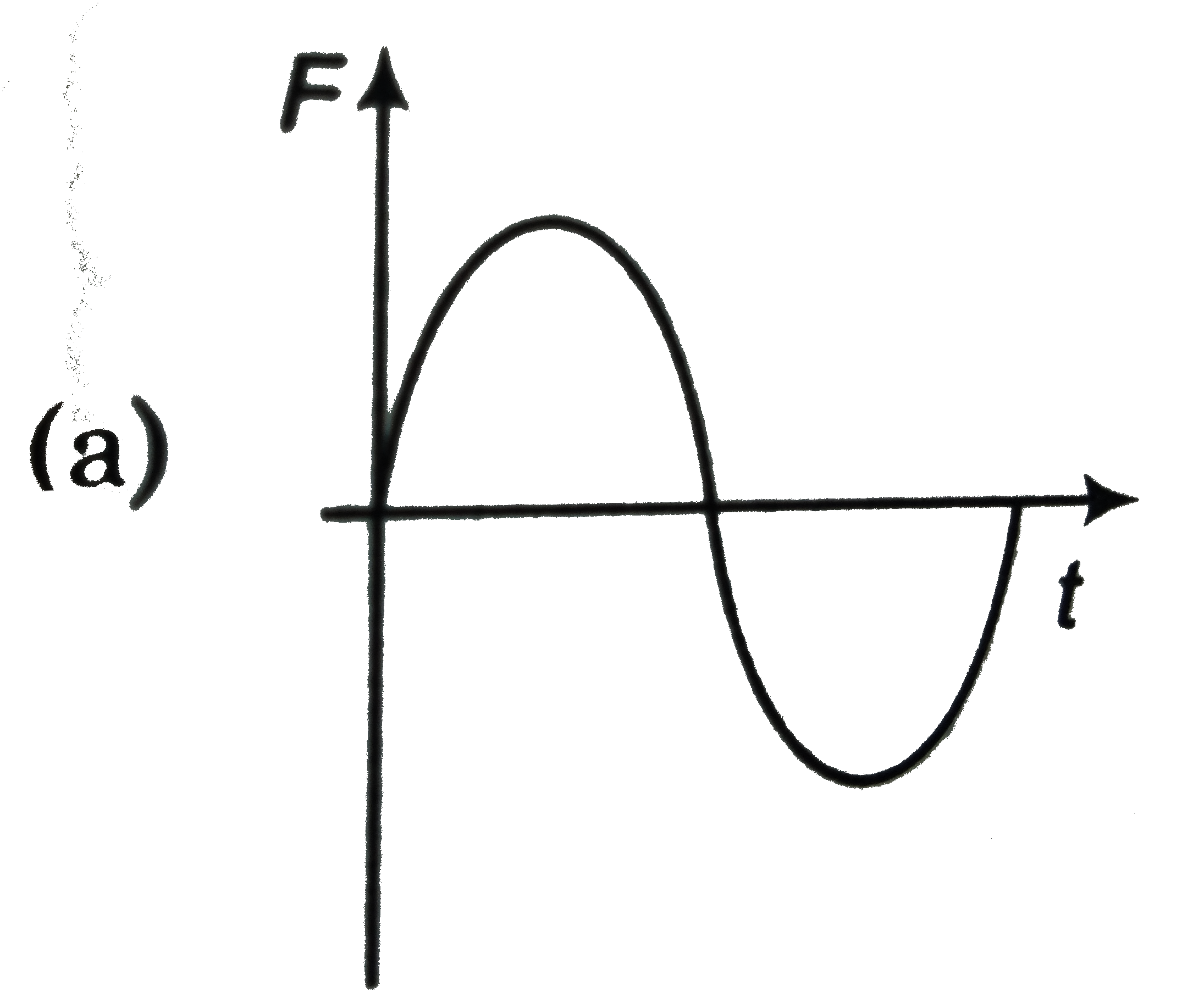
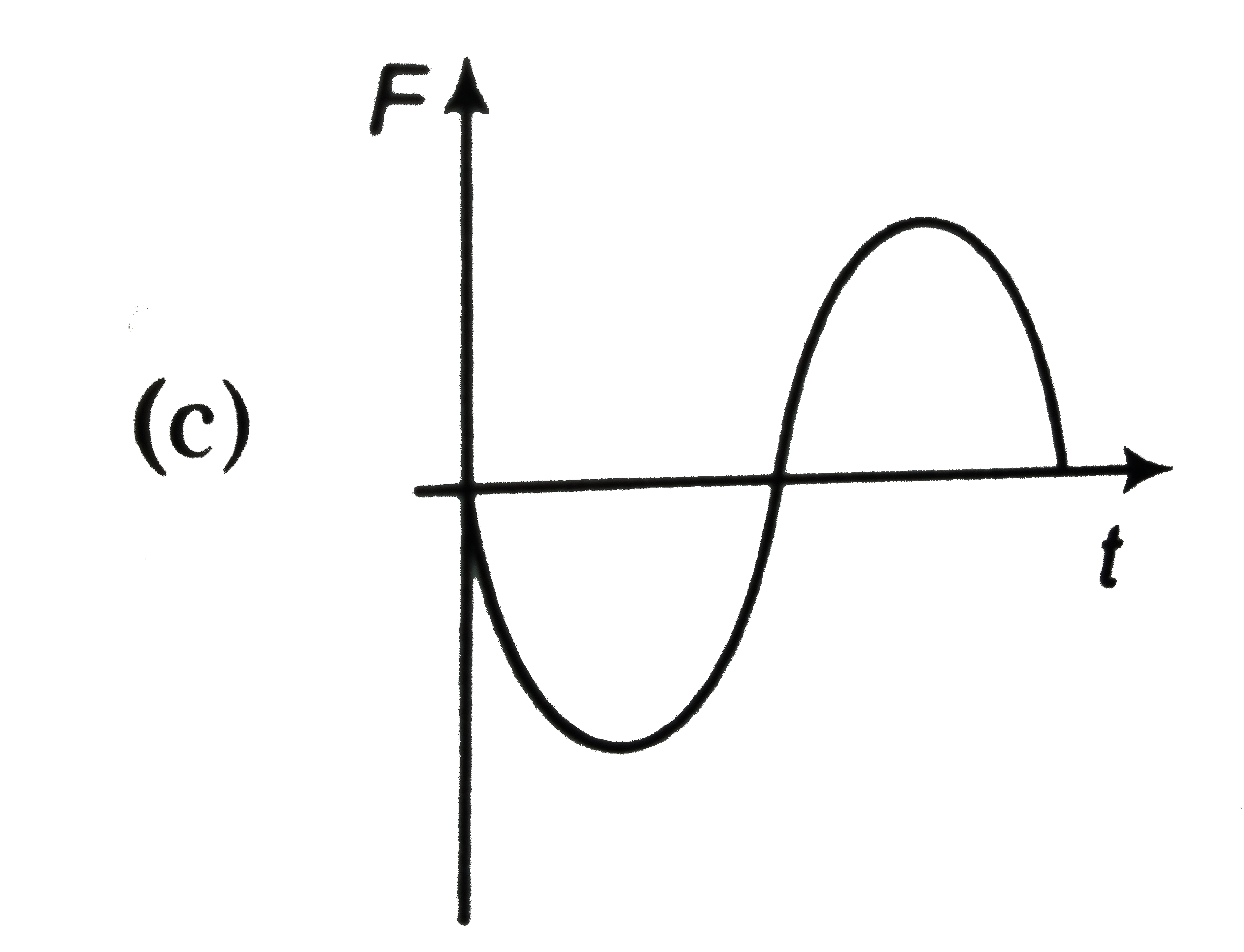
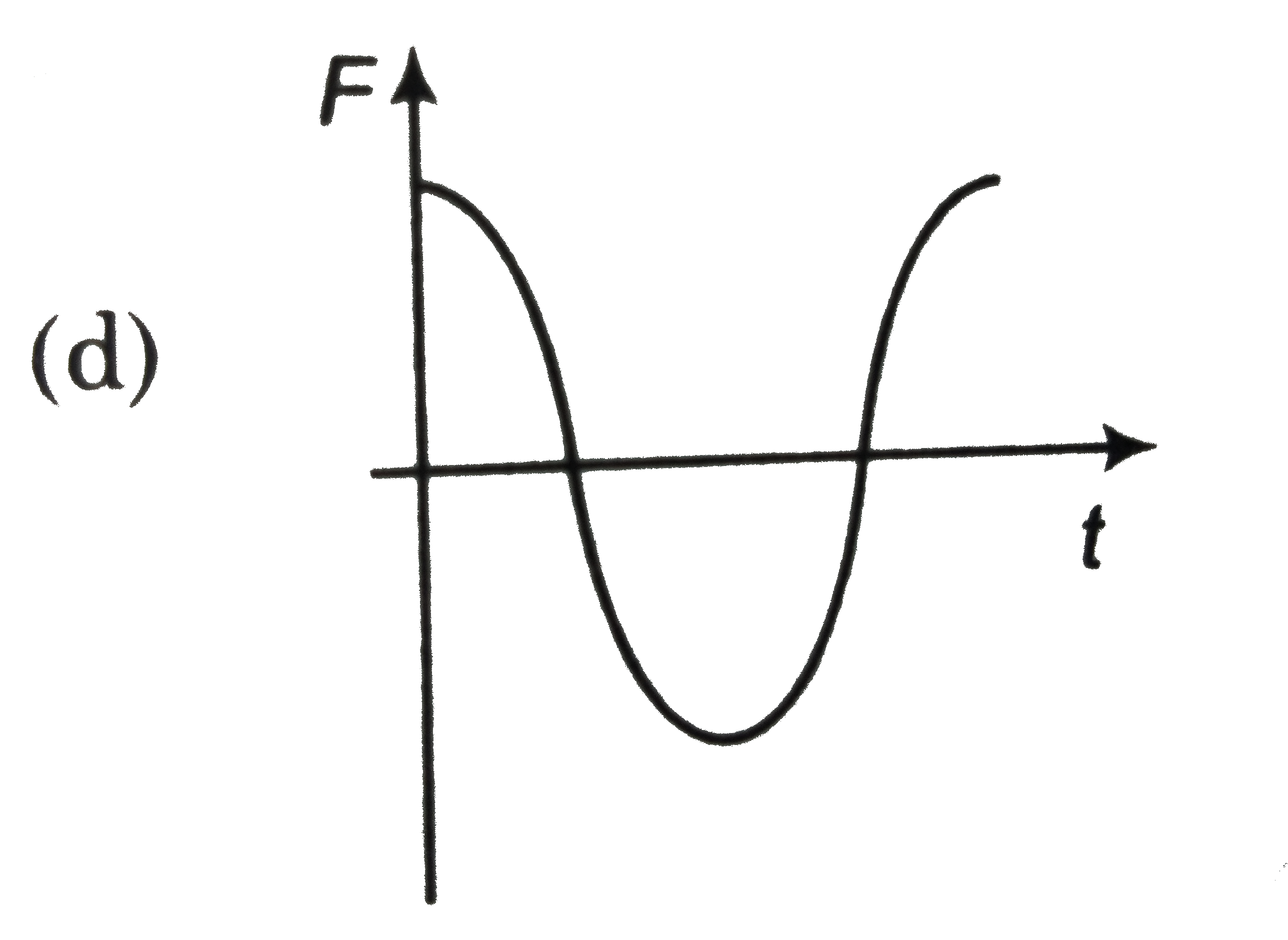
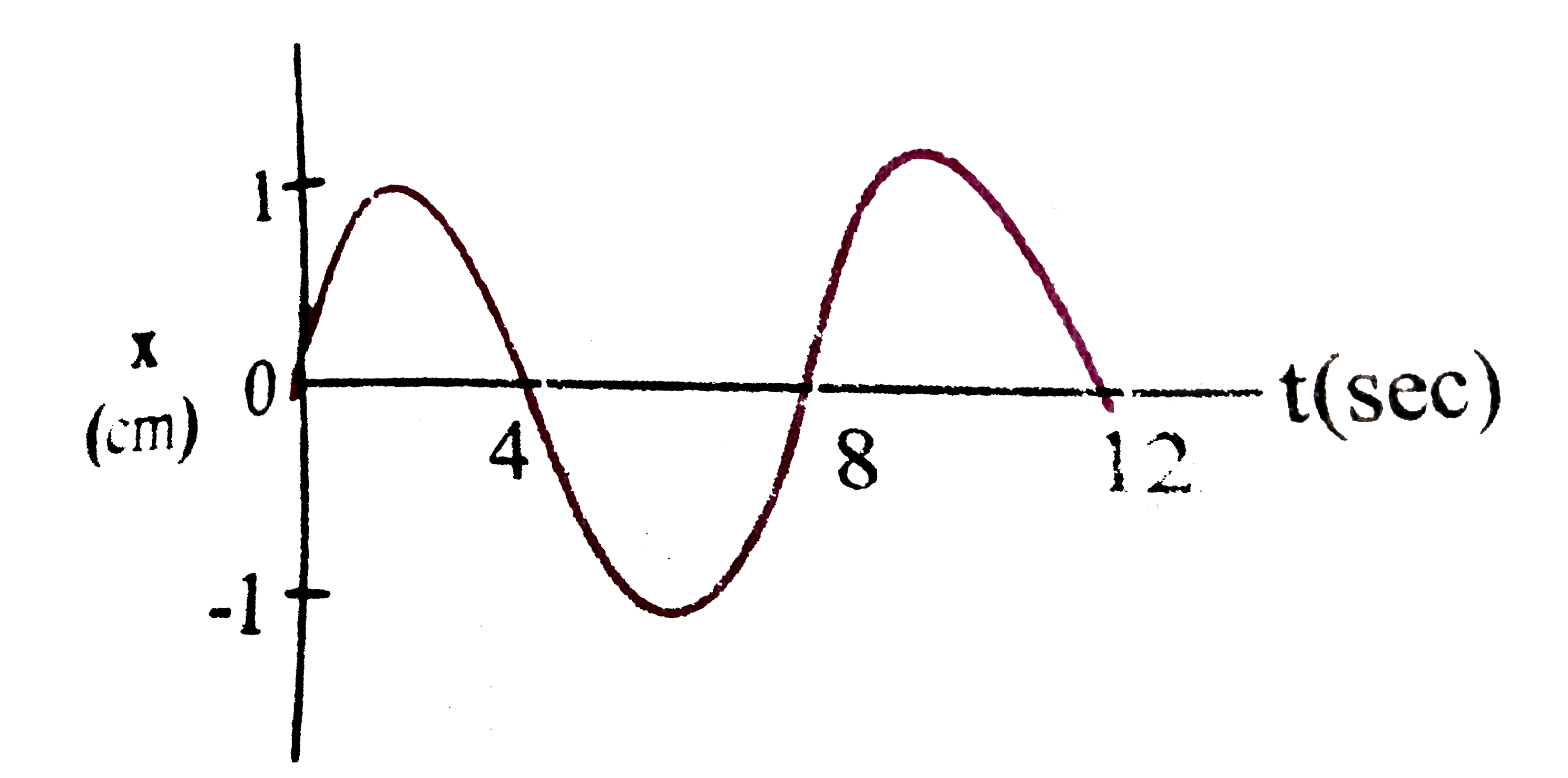
The displacement - time (x−t) graph of a particle executing simple harmonic motion is shown in figure. The correct variation of net force F action on the particle as a function of time is

A
B

C
D
Video Solution
Text Solution
The correct Answer is:B
x=Acosωt
F∝−x
Hence, F is −cosωt graph.
|
Similar Questions
Knowledge Check
The velocity of a particle executing simple harmonic motion is
Aω2√A2+x2Bω√A2−x2Cω√A2+x2Dω2√A2−x2While a particle executes linear simple harmonic motion
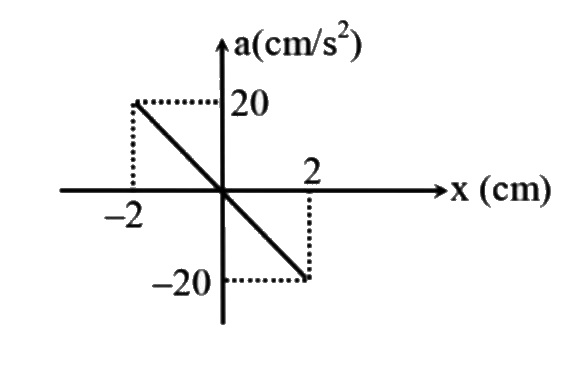
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.Dits linear velocity and acceleration always attain their peak values simlataneaously.The acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
A4π√3sB2π√3sCThe given graph doesn't represent simple harmonic motionDinformation is insufficient
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is

View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is

View Solution