The electric field near a conducting surface having a uniform surface charge denstiy σ is given by
(a) σε0 and is parallel to the surface
(b) 2σε0
(c) σε0 and is normal to the surface
(d) 2σε0 and is normal to the surface
The correct Answer is:C
To solve the problem of finding the electric field near a conducting surface with a uniform surface charge density σ, we can follow these steps:
1. Understanding the Problem:
We have a conducting surface with a uniform surface charge density σ. We need to determine the electric field E near this surface.
2. Choosing a Gaussian Surface:
To apply Gauss's law, we will consider a Gaussian surface. A suitable choice is a cylindrical Gaussian surface that straddles the conducting surface. This surface will have one flat face inside the conductor and one flat face outside.
3. Applying Gauss's Law:
According to Gauss's law, the electric flux ΦE through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
ΦE=Qϵ0
The electric flux ΦE is given by:
ΦE=E⋅A
where E is the electric field and A is the area of the Gaussian surface.
4. Calculating the Charge Enclosed:
The charge Q enclosed by the Gaussian surface can be calculated using the surface charge density σ:
Q=σ⋅A
5. Setting Up the Equation:
Substituting the expression for Q into Gauss's law gives:
E⋅A=σ⋅Aϵ0
6. Solving for the Electric Field E:
We can cancel A from both sides (assuming A≠0):
E=σϵ0
7. Direction of the Electric Field:
The electric field E is directed perpendicular to the surface of the conductor and away from the surface if the charge is positive.
Final Answer:
The electric field near a conducting surface having a uniform surface charge density σ is given by:
E=σϵ0
We have a conducting surface with a uniform surface charge density σ. We need to determine the electric field E near this surface.
To apply Gauss's law, we will consider a Gaussian surface. A suitable choice is a cylindrical Gaussian surface that straddles the conducting surface. This surface will have one flat face inside the conductor and one flat face outside.
According to Gauss's law, the electric flux ΦE through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
ΦE=Qϵ0
The electric flux ΦE is given by:
ΦE=E⋅A
where E is the electric field and A is the area of the Gaussian surface.
The charge Q enclosed by the Gaussian surface can be calculated using the surface charge density σ:
Q=σ⋅A
Substituting the expression for Q into Gauss's law gives:
E⋅A=σ⋅Aϵ0
We can cancel A from both sides (assuming A≠0):
E=σϵ0
The electric field E is directed perpendicular to the surface of the conductor and away from the surface if the charge is positive.
The electric field near a conducting surface having a uniform surface charge density σ is given by:
E=σϵ0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Assertion Mass of ion is slightly differed from its element.
Reason Ion is formed, when some electrons are removed or added, so mass changes.
View SolutionMatch the following two columns.
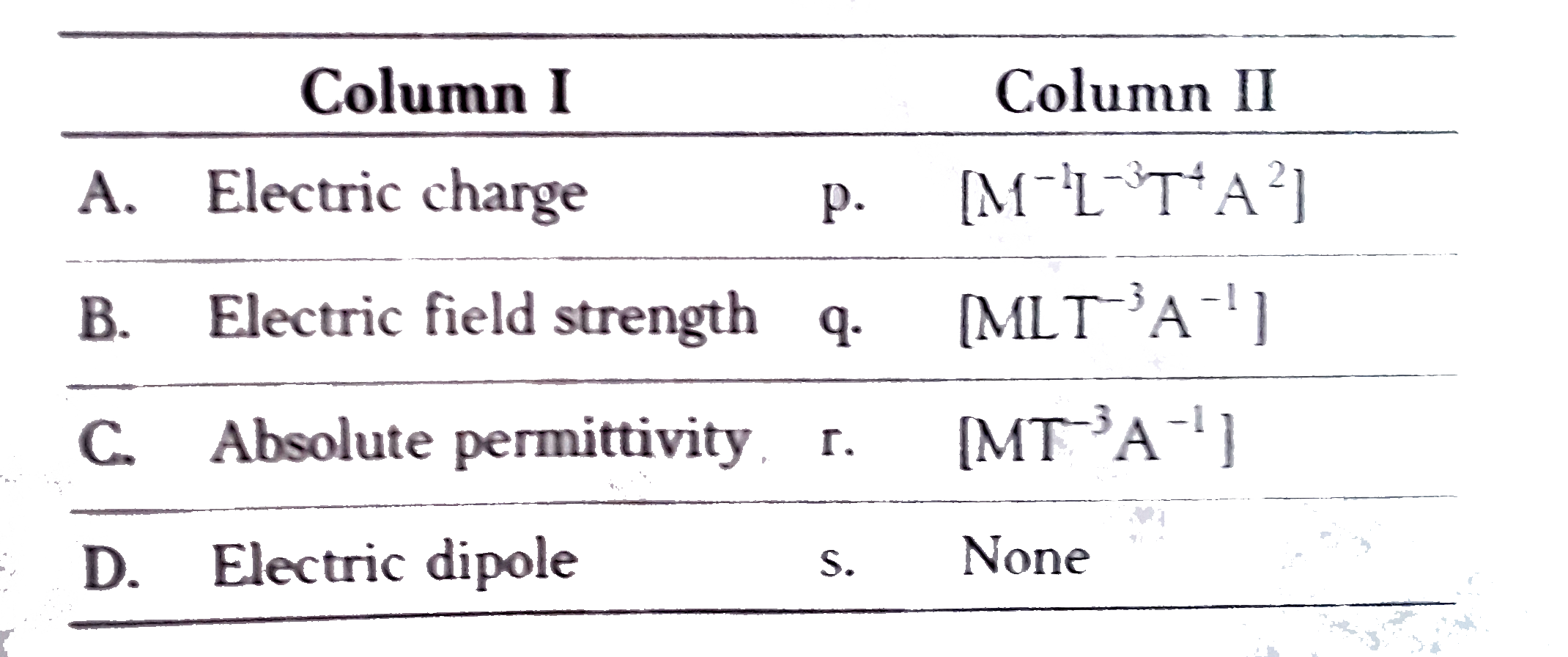
View SolutionThe law goverening electrostatics is coulomb's law.In priciple coulomb's law can be used to compute electric field due to any charge configuation .In pracitce however it is a formidable task to compute electric field due to uniform charge distributions .For such cases Gauss proposed a theorem which states that
∮¯¯¯E.¯¯¯¯ds=qε0
where ds is an element of area directed across the outward normal for the surface at every point .The integral is called electric flux.Any convenient surface that we choose to evalute the surface integral is called the Gaussian surface.
The SI unit of electric flux is
View SolutionA capacitor of 2μF is charged as shown in the figure. When the switch S is turned to position 2, the percentage of its stored energy dissipated is

View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionElectric field intensity at a point due to an infinite sheet of charge having surface charge density sigma is E .If sheet were conducting electric intensity would be
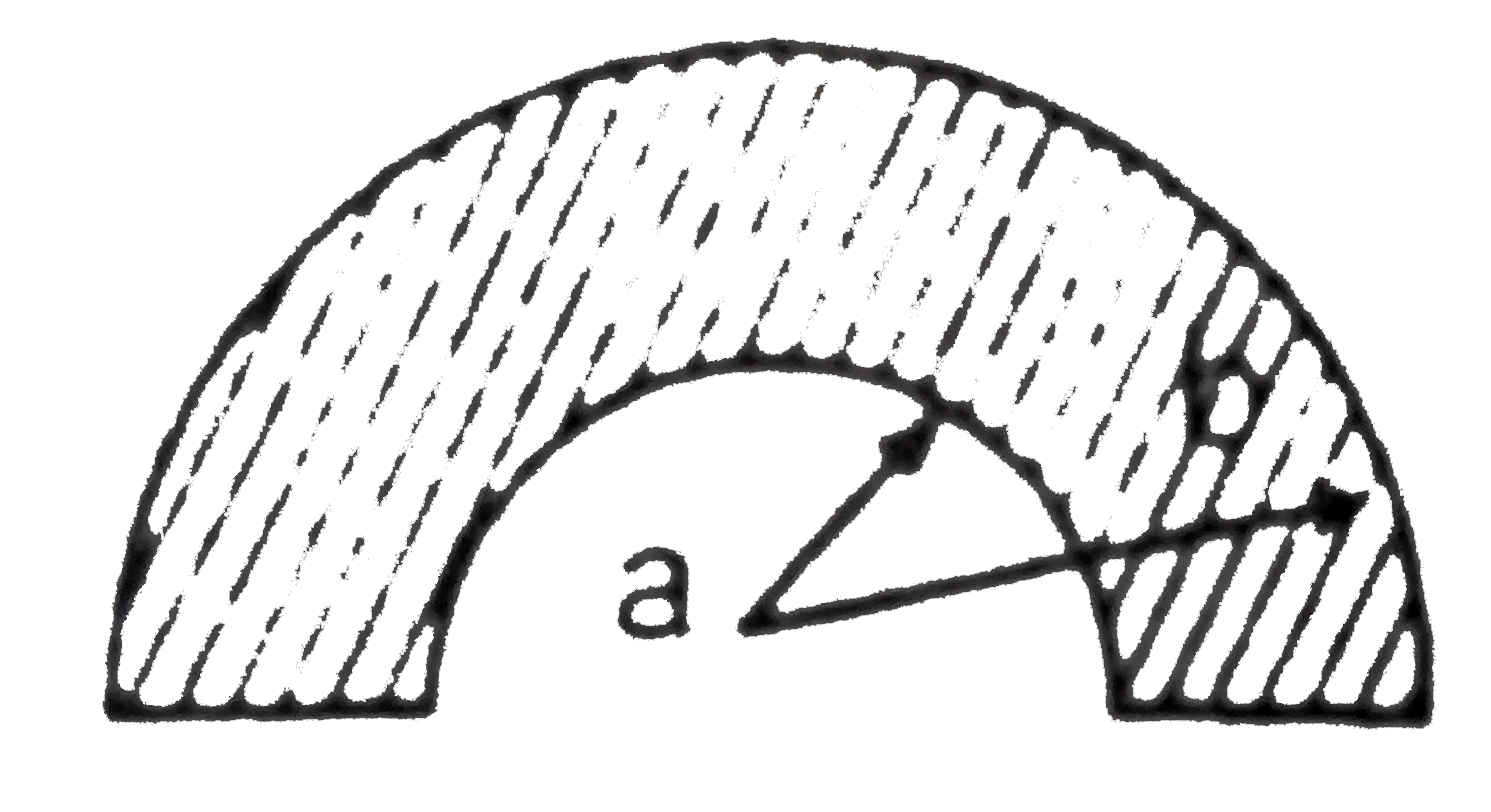
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionThe electric field near a conducting surface having a uniform surface charge denstiy σ is given by
View SolutionThe electric intensity at a point near a charged conductor of surface charge density sigma is
View Solutionएकसमान पृष्ठ आवेश धनत्व σ वाले चालक पृष्ठ के निकट विद्युत क्षेत्र होता है :
View SolutionWhat is electric field near the surface of a non-conducting charged surface?
View SolutionElectric field at a point near a uniformaly charged infinite plane sheet having surface density of charge sigma is given as E= ________________
View SolutionElectric field due to an infinite sheet of charge having surface charge density sigma is E. Electric field due to an infinite conducting sheet of same surface density of charge is
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionElectric field due to an infinite sheet of charge having surface density σ is E Electric field due to an infinite conducting sheet of same surface density of charge is
View Solution

