The electron in a hydrogen atom makes a transition n1→n2, where n1 and n2 are the principle quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. the possible values of n1 and n2 are
n1Δn2=2
n18,n2=2
n1Δ,n2=1
n1=6,n2=2
The correct Answer is:A
To solve the problem, we will use the Bohr model of the hydrogen atom and the relationship between the time period of the electron in different energy states.
1. Understanding the Time Period in Bohr Model:
The time period T of an electron in a hydrogen atom is given by the formula:
T∝n3
where n is the principal quantum number.
2. Setting Up the Ratio of Time Periods:
According to the problem, the time period of the electron in the initial state T1 is 8 times that in the final state T2:
T1=8T2
3. Expressing Time Periods in Terms of Quantum Numbers:
Using the proportionality we established:
T1∝n31andT2∝n32
Therefore, we can write:
T1T2=n31n32
4. Substituting the Known Ratio:
Substituting T1=8T2 into the ratio gives:
8=n31n32
5. Rearranging the Equation:
Rearranging the equation, we have:
n31=8n32
6. Taking Cube Roots:
Taking the cube root of both sides results in:
n1=2n2
7. Finding Possible Values of n1 and n2:
Now we need to find pairs of n1 and n2 that satisfy n1=2n2. We can check the options provided:
- Option A: n1=6,n2=3 → 6=2×3 (Valid)
- Option B: n1=8,n2=2 → 8≠2×2 (Invalid)
- Option C: n1=4,n2=1 → 4≠2×1 (Invalid)
- Option D: n1=6,n2=2 → 6≠2×2 (Invalid)
8. Conclusion:
The only valid option is:
n1=6andn2=3
Final Answer:
The possible values of n1 and n2 are n1=6 and n2=3.
The time period T of an electron in a hydrogen atom is given by the formula:
T∝n3
where n is the principal quantum number.
According to the problem, the time period of the electron in the initial state T1 is 8 times that in the final state T2:
T1=8T2
Using the proportionality we established:
T1∝n31andT2∝n32
Therefore, we can write:
T1T2=n31n32
Substituting T1=8T2 into the ratio gives:
8=n31n32
Rearranging the equation, we have:
n31=8n32
Taking the cube root of both sides results in:
n1=2n2
Now we need to find pairs of n1 and n2 that satisfy n1=2n2. We can check the options provided:
- Option A: n1=6,n2=3 → 6=2×3 (Valid)
- Option B: n1=8,n2=2 → 8≠2×2 (Invalid)
- Option C: n1=4,n2=1 → 4≠2×1 (Invalid)
- Option D: n1=6,n2=2 → 6≠2×2 (Invalid)
The only valid option is:
n1=6andn2=3
The possible values of n1 and n2 are n1=6 and n2=3.
Topper's Solved these Questions
- ATOMSBook:DC PANDEY ENGLISHChapter:ATOMSExercise:ASSERTION AND REASON
Explore 10 Videos
- ATOMSBook:DC PANDEY ENGLISHChapter:ATOMSExercise:MATCH THE COLUMNS
Explore 4 Videos
- ATOMSBook:DC PANDEY ENGLISHChapter:ATOMSExercise:Check point 12.3
Explore 15 Videos
- ALTERNATING CURRENTBook:DC PANDEY ENGLISHChapter:ALTERNATING CURRENTExercise:JEE MAIN
Explore 62 Videos
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
Similar Questions
Assertion: Angular momentum of single electron in any orbit or hydrogen type atom is independent of the atomic number of the element.
Reason: In ground state angular momentum is minimum
View SolutionIn Column I physical quantities corresponding to hydrogen and hydrogen like atom are given. In column II, powers of principal quantum number n are givem on which thosee physical quantities depend. Match the two columns.
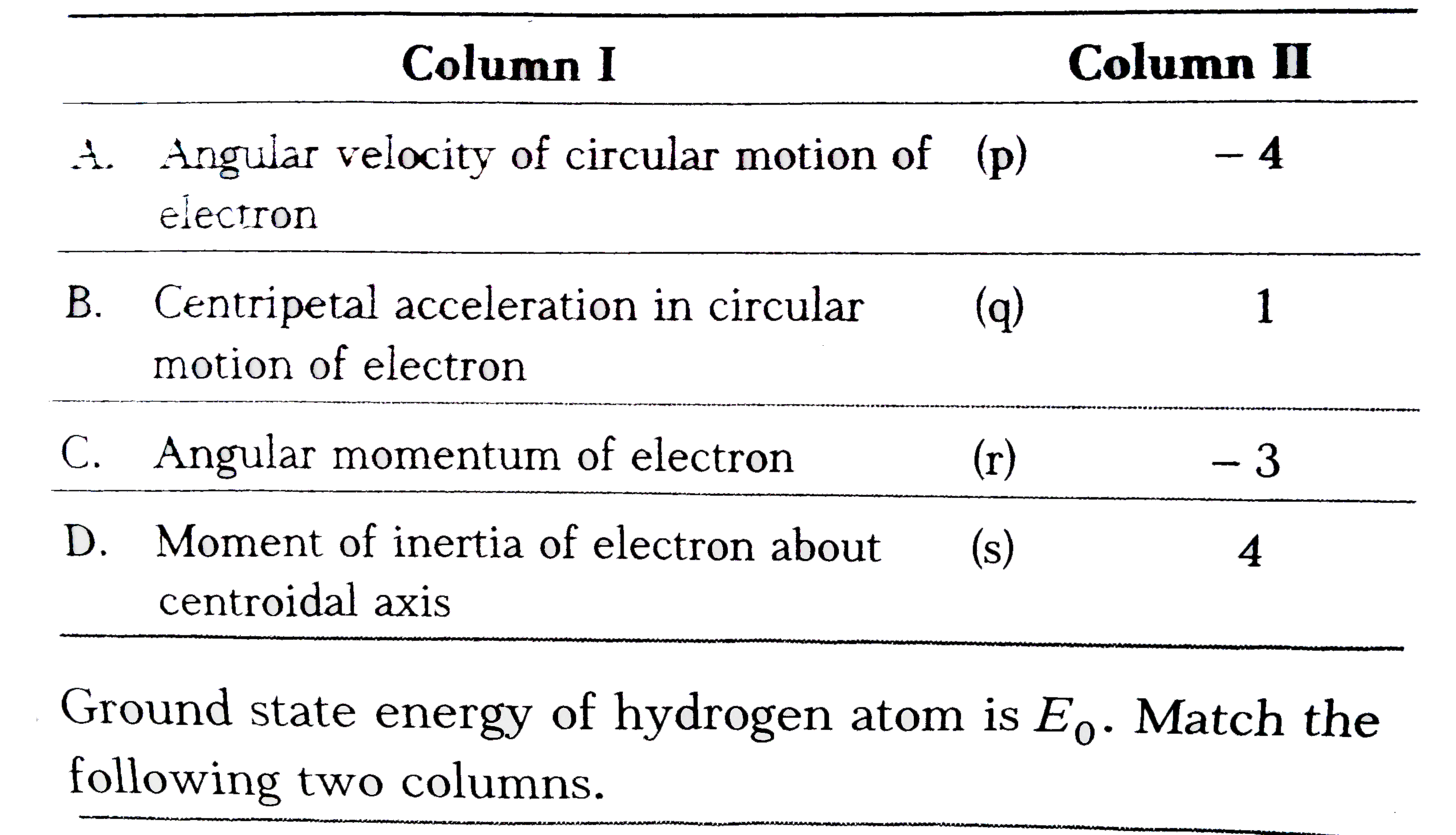
View SolutionX-rays were discovered by
View SolutionIn the given arrangement, the loop is moved with consisant velocity in uniform magnetic field B in a restricted a region of width a. The time for which the emf is induced in the cirucit is

View SolutionIn the circuit shown as potential difference of 60V is appliled across AB. The potential difference between the points M and N is
View SolutionThe electron in a hydrogen atom make a transtion n_(1) rarr n_(2) where n_(1) and n_(2) are the priocipal quantum number of the two states . Assume the Bohr model to be valid . The time period of the electron in the initial state is eight time that in the state . THe possible values of n_(1) and n_(2) are
View SolutionThe electron in a hydrogen atom makes a trapsition n_(1) to n_(2), where n_(1) and n_(2) are the principal quantum numbers of the two energy states. Assume Bohr's model to be velid. The time period of the electron in the initial state is eight time that in the final static. what are the possible value of n_(1) and n_(2) ?
View SolutionThe electron in a hydrogen atom makes a transition n1→n2 where n1 and n2 are the principal qunatum numbers of the two states. Assume the Bohr model to be valid. The frequency of orbital motion of the electron in the initial state is 1/27 of that in the final state. The possible values of n1 and n2 are
View SolutionAn electron in a hydrogen atom makes a transition from n_(1) to n_(2) . If the time period of electron in the initial state is eight times that in the final state then Find the ratio n_(1)/n_(2)
View SolutionThe electron in a hydrogen atom makes a transition from n = n_(1) to n = n_(2) state. The time period of the electron in the initial state (n_(1)) is eight times that in the final state (n_(2)) The possible values of n_(1) and n_(2) are
View SolutionAn electron in a hydrogen atom makes a transition nl→n2, where n1andn2 are principal quantum numbers of the states. Assume the Bohr's model to be valid. The time period of the electron in the initial state is eight times to that of final state. What is ratio of n2/n2
View SolutionAn electron in a hydrogen atom makes a transition nl→n2, where n1andn2 are principal quantum numbers of the states. Assume the Bohr's model to be valid. The time period of the electron in the initial state is eight times to that of final state. What is ratio of n2/n2
View SolutionAn electron in a hydrogen atom makes a transition nl→n2, where n1andn2 are principal quantum numbers of the states. Assume the Bohr's model to be valid. The time period of the electron in the initial state is eight times to that of final state. What is ratio of n2/n2
View SolutionThe electron in a hydrogen atom makes a transition from n = n_(1) to n = n_(2) state. The time period of the electron in the initial state is eight times that in the electron in the initial state is eight times that is the final state. The possible values of n_(1) and n_(2) are
View SolutionThe electron in a hydrogen atom makes a transition n1→n2, where n1 and n2 are the principle quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. the possible values of n1 and n2 are
View Solution
